题目内容
不等式log2(2x-1)•log2(2x+1-2)<2的解集为
- A.
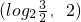
- B.
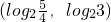
- C.(-2,1)
- D.
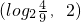
B
分析:先将log2(2x-1)看作一个整体,将问题转化为一元二次不等式问题,由此即可获得log2(2x-1)的范围,进而利用对数函数、指数函数的性质解得x的范围
解答:设t=log2(2x-1),则不等式可化为t(t+1)<2,
所以t2+t-2<0
所以-2<t<1.
所以-2<log2(2x-1)<1,
所以2-2<2x-1<2
所以 <2x<3
<2x<3
所以解集为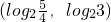
故选B.
点评:本题考查的是对数函数图象与性质的综合应用问题.解答的关键是换元,将对数不等式问题转化为一元二次不等式问题.注意正确运用指数函数、对数函数的性质,合理转化.
分析:先将log2(2x-1)看作一个整体,将问题转化为一元二次不等式问题,由此即可获得log2(2x-1)的范围,进而利用对数函数、指数函数的性质解得x的范围
解答:设t=log2(2x-1),则不等式可化为t(t+1)<2,
所以t2+t-2<0
所以-2<t<1.
所以-2<log2(2x-1)<1,
所以2-2<2x-1<2
所以
 <2x<3
<2x<3所以解集为
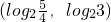
故选B.
点评:本题考查的是对数函数图象与性质的综合应用问题.解答的关键是换元,将对数不等式问题转化为一元二次不等式问题.注意正确运用指数函数、对数函数的性质,合理转化.

练习册系列答案
相关题目