题目内容
已知函数f（x）=2asin2x+2sinxcosx-a（a为常数）在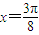
处取得最大值（1）求a的值；
（2）求f（x）在[0，π]上的增区间．
【答案】分析：（1）化简f（x）=sin2x-acos2x，由题意可得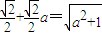
，解得a的值．
（2）利用两角差的正弦公式可得f（x）=
，由
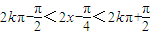求得x的范围即得f（x）的增区间，再由x∈[0，π]，进一步确定f（x）在[0，π]上的
增区间．
解答：解：（1）f（x）=2sinxcosx-a（1-2sin2x）=sin2x-acos2x…（2分）
由题意：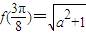
，即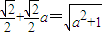
，…（4分） 解得a=1…（6分）
（2）
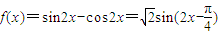．…（8分）
由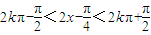
，解得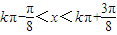
，k∈Z…（10分）
所以f（x）在[0，π]上的增区间为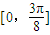
，
． …（12分）
点评：本题主要考查两角和差的正弦公式，二倍角公式，正弦函数的单调性的应用，属于中档题．
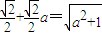，解得a的值．（2）利用两角差的正弦公式可得f（x）=
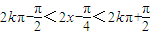，由求得x的范围即得f（x）的增区间，再由x∈[0，π]，进一步确定f（x）在[0，π]上的增区间．
解答：解：（1）f（x）=2sinxcosx-a（1-2sin2x）=sin2x-acos2x…（2分）
由题意：
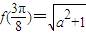，即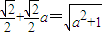，…（4分） 解得a=1…（6分）（2）
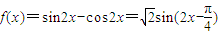．…（8分）由
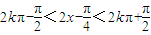，解得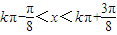，k∈Z…（10分）所以f（x）在[0，π]上的增区间为
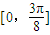，． …（12分）点评：本题主要考查两角和差的正弦公式，二倍角公式，正弦函数的单调性的应用，属于中档题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目