Question

（2010•上海模拟）如图，四棱锥P-ABCD的底面ABCD是平行四边形，PF⊥平面ABCD，垂足F在AD上，且AF=

1

3

FD，FB⊥FC，FB=FC=2，E是BC的中点，四面体P-BCF的体积为

8

3

．
（1）求异面直线EF和PC所成的角；
（2）求点D到平面PBF的距离．

Answer 1

分析：解法一：向量法．首先利用PF⊥平面ABCD的特点，以F点为原点，建立适当的空间直角坐标系，利用向量来求异面直线的夹角、点到面的距离．其中该异面直线的夹角可以转换为

FE

与

PC

的夹角来求，点D到面PBF的距离是d=|

FD

 •

n0

|
解法二：定义法．利用平行关系作出异面直线EF与PC所成的角，利用几何关系找出点D到PBF的距离．

解答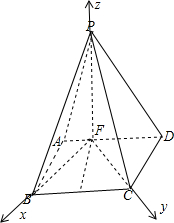：解：（解法一）
（1）由已知VP-BCF= 

1

3

S△BCF•PF=

1

3

•

1

2

• BF•CF•PF=

8

3

∴PF=4
如图所示以F为原点以

FB

，

FC

，

FP

所在直线为x，y，z轴，建立空间直角坐标系o-xyz
则B（2，0，0），C（0，2，0），P（0，0，4），由E是BC的中点，故E（1，1，0）
∴

FE

=(1，1，0)，

PC

=(0，2，-4)
∴cos＜

PE

，

PC

＞=

PE • PC

| PE || PC |

=

2

2 × 20

=

10

10

∴异面直线EF和PC所成的角arccos

10

10

（2）平面PBF的单位法向量

n0

=（0，1，0）
∵

FD

=

3

4

BC

= (-

3

2

，

3

2

，0)
∴点D到面PBF的距离是d=|

FD

 •

n0

|=

3

2

（解法二）
（1）由已知VP-BCF= 

1

3

S△BCF•PF=

1

3

•

1

2

• BF•CF•PF=

8

3

∴PF=4
在平面ABCD内，过C做CH∥EF，交AD于H，连接PH
则∠PCH（或其补角）就是异面直线EF与PC所成的角
在△PCH中，CH=

2

，PC=

20

，PH=

18

由余弦定理可得cos∠PCH=

10

10

∴异面直线EF和PC所成的角为arccos

10

10

（2）∵PF⊥平面ABCD，PF?平面PBA
∴平面PBF⊥平面ABCD
在平面ABCD内过D作DK⊥BF，交BF延长线与K，则DK⊥平面PBF
∴DK的长就是点D到平面PBF的距离
∵BC=2

2

∴DF=

3

4

AD=

3

4

BC=

3

2

2

∵在△DFK中DK=DFsin45°=

3

2

∴点D到平面PBF的距离为

3

2

点评：此题考查了运用向量法或定义法来求异面直线的夹角和点到面的距离，属必考题，较难．解题的关键是在运用向量法时应注意异面直线的夹角的转化，以及点到面的距离的向量公式！