题目内容
(14分)已知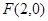 ,直线
,直线 ,
,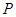 为平面上的动点,过点
为平面上的动点,过点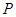 作
作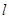 的垂线,垂足为点
的垂线,垂足为点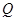 ,且
,且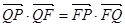 .
.
(1)求动点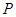 的轨迹
的轨迹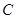 的方程;
的方程;
(2)过点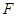 的直线交轨迹
的直线交轨迹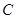 于
于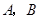 两点,点O是直角坐标系的原点,求
两点,点O是直角坐标系的原点,求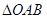 面积的最小值,并求出当
面积的最小值,并求出当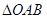 的面积取到最小值时直线
的面积取到最小值时直线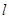 的方程。
的方程。
【答案】
(1)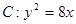 (2)
(2) 面积的最小值为2,此时直线
面积的最小值为2,此时直线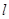 的方程为
的方程为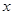 =1
=1
【解析】
试题分析:(1)设点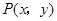 ,则
,则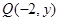 ,
,
由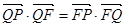 得:
得: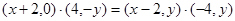 ,
,
化简得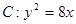 . ……6分
. ……6分
(2)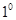 当直线
当直线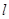 与
与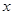 轴垂直时,
轴垂直时,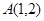 、
、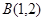 ,
,
所以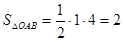 ; ……8分
; ……8分
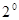 当直线
当直线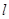 与
与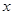 轴不垂直时,可设直线
轴不垂直时,可设直线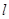 的方程为
的方程为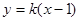 ,
,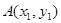 、
、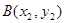 ,
,
将抛物线方程与直线方程联立,消去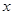 整理得:
整理得: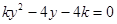 ,
,
所以有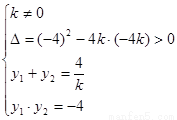 ,
,
所以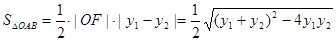 =
=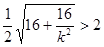 , ……13分
, ……13分
所以 面积的最小值为2,此时直线
面积的最小值为2,此时直线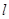 的方程为
的方程为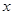 =1。 ……14分
=1。 ……14分
考点:本小题主要考查平面向量的数量积运算、抛物线标准方程的求解、直线与抛物线的位置关系和三角形面积公式的应用以及最值的求解,考查学生分析问题、解决问题的能力和运算求解能力.
点评:设直线方程时,一定要考虑斜率是否存在两种情况,否则会漏掉一个解.

练习册系列答案
相关题目