题目内容
(本小题满分12分)
设函数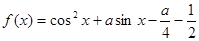 .
.
(1)当  ≤
≤ ≤
≤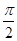 时,用
时,用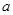 表示
表示 的最大值
的最大值 ;
;
(2)当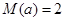 时,求
时,求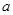 的值,并对此
的值,并对此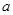 值求
值求 的最小值;
的最小值;
(3)问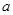 取何值时,方程
取何值时,方程 =
=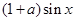 在
在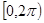 上有两解?
上有两解?
(1)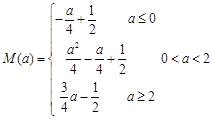 (2)
(2)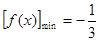 .
.
(3) 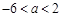 ,
,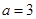 .
.
解析试题分析:(1) 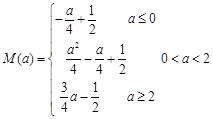 (
(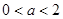 ) (
) ( )
)
(2) 将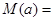
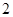 代入(
代入( )式, 得
)式, 得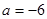 或
或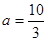 .
.
当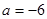 时,
时, 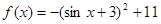
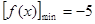 ;
;
当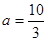 时,
时, 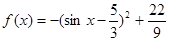
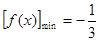 .
.
(3) 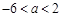 ,
,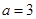 .
.
考点:本试题考查了函数与方程的知识。
点评:解决该试题的关键是对于函数的最值,要理解分段函数的最值的准确理解和运用,同时对于方程根的问题,可以运用分离参数 思想来得到。属于中档题。

练习册系列答案
相关题目
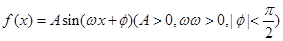 在一个周期内的图象下图所示。
在一个周期内的图象下图所示。
 ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。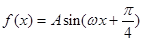 (其中
(其中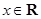 ,
,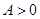 ,
, )的最大值为2,最小正周
)的最大值为2,最小正周 .
.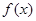 的解析式;
的解析式;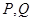 的横坐标依次为
的横坐标依次为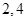 ,
, 为坐标原点,求△
为坐标原点,求△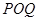 的
的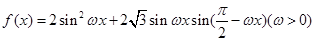 最小正周期为
最小正周期为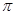
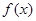 的单调递增区间及对称中心坐标
的单调递增区间及对称中心坐标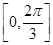 上的取值范围。
上的取值范围。
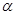 为第三象限角,
为第三象限角,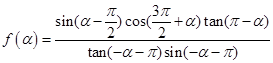 .
.
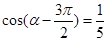 ,求
,求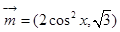 ,
,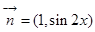 ,函数
,函数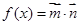 .
. 的最小正周期和单调增区间;
的最小正周期和单调增区间;
 中,
中,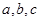 分别是角
分别是角 的对边,R为
的对边,R为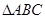 外接圆的半径,且
外接圆的半径,且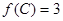 ,
,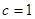 ,
,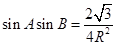 ,且
,且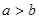 ,求
,求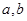 的值.
的值.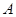 是三角形的内角,且
是三角形的内角,且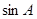 和
和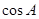 是关于
是关于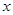 方程
方程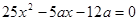 的两个根。
的两个根。 的值;(6分)
的值;(6分)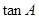 的值.(6分)
的值.(6分)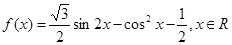
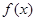 的最小正周期;
的最小正周期; 上的单调性并求在此区间上
上的单调性并求在此区间上