题目内容
下列各命题中,不正确的是( )A.若f(x)是连续的奇函数,则

B.若f(x)是连续的偶函数,则

C.若f(x)在[a,b]上连续且恒正,则

D.若f(x)在[a,b]上连续,且
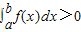 ,则f(x)在[a,b]上恒正
,则f(x)在[a,b]上恒正
【答案】分析:A..若f(x)是连续的奇函数,则 =
= ,据此即可判断出答案;
,据此即可判断出答案;
B.若f(x)是连续的偶函数,则 =
= ,据此即可判断出答案;
,据此即可判断出答案;
C.因为f(x)在[a,b]上连续且恒正,根据其单调性即可判断出是否正确;
D.举出反例即可否定.
解答:解:A.∵f(x)是连续的奇函数,∴ =
= +
+ =-
=-
 =0,故A正确;
=0,故A正确;
B.∵f(x)是连续的偶函数,∴ =
=
 =2
=2 ,故B正确;
,故B正确;
C.∵f(x)在[a,b]上连续且恒正,∴ ,故C正确;
,故C正确;
D.举反例: =
= =4-
=4- ,而f(x)=x3在区间[-1,0)上恒小于0,即函数f(x)在区间[-1,2]上不恒为正,故D不正确.
,而f(x)=x3在区间[-1,0)上恒小于0,即函数f(x)在区间[-1,2]上不恒为正,故D不正确.
综上可知:只有D不正确.
故选D.
点评:正确理解定积分的性质是解题的关键.
 =
= ,据此即可判断出答案;
,据此即可判断出答案;B.若f(x)是连续的偶函数,则
 =
= ,据此即可判断出答案;
,据此即可判断出答案;C.因为f(x)在[a,b]上连续且恒正,根据其单调性即可判断出是否正确;
D.举出反例即可否定.
解答:解:A.∵f(x)是连续的奇函数,∴
 =
= +
+ =-
=-
 =0,故A正确;
=0,故A正确;B.∵f(x)是连续的偶函数,∴
 =
=
 =2
=2 ,故B正确;
,故B正确;C.∵f(x)在[a,b]上连续且恒正,∴
 ,故C正确;
,故C正确;D.举反例:
 =
= =4-
=4- ,而f(x)=x3在区间[-1,0)上恒小于0,即函数f(x)在区间[-1,2]上不恒为正,故D不正确.
,而f(x)=x3在区间[-1,0)上恒小于0,即函数f(x)在区间[-1,2]上不恒为正,故D不正确.综上可知:只有D不正确.
故选D.
点评:正确理解定积分的性质是解题的关键.

练习册系列答案
相关题目
 是连续的奇函数,则
是连续的奇函数,则

 上连续且恒正,则
上连续且恒正,则