题目内容
(2007•武汉模拟)若AB过椭圆
+
=1 中心的弦,F1为椭圆的焦点,则△F1AB面积的最大值为( )
| x2 |
| 25 |
| y2 |
| 16 |
分析:先设A的坐标(x,y)则根据对称性得:B(-x,-y),再表示出△F1AB面积,由图知,当A点在椭圆的顶点时,其△F1AB面积最大,最后结合椭圆的标准方程即可求出△F1AB面积的最大值.
解答: 解:设A的坐标(x,y)则根据对称性得:B(-x,-y),
解:设A的坐标(x,y)则根据对称性得:B(-x,-y),
则△F1AB面积S=
OF×|2y|=c|y|.
∴当|y|最大时,△F1AB面积最大,
由图知,当A点在椭圆的顶点时,其△F1AB面积最大,
则△F1AB面积的最大值为:cb=
×4=12.
故选B.
 解:设A的坐标(x,y)则根据对称性得:B(-x,-y),
解:设A的坐标(x,y)则根据对称性得:B(-x,-y),则△F1AB面积S=
| 1 |
| 2 |
∴当|y|最大时,△F1AB面积最大,
由图知,当A点在椭圆的顶点时,其△F1AB面积最大,
则△F1AB面积的最大值为:cb=
| 25-16 |
故选B.
点评:本小题主要考查函数椭圆的标准方程、椭圆的简单性质、面积公式等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
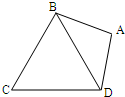 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=