题目内容
(2007•武汉模拟)已知函数f(x)=2
+
,则函数f(x)的值域为( )
| x |
| 4-x |
分析:先根据x+4-x=4,与x无关,结合三角恒等式:sin2θ+cos2θ=1,观察相似之处,便可利用换元法;设
=2sinα,
=2cosα,再结合辅助角公式以及三角函数的图象即可得到答案.
| x |
| 4-x |
解答:解:设
=2sinα,
=2cosα,α∈[0,
].
则f(x)=4sinα+2cosα=2
sin(α+arctan2).
根据三角函数图象,当α+arctan2=
时f(x)取得最大值2
;
当α=0时f(x)取得最小值2.
∴f(x)的值域为[2,2
].
故选:D.
| x |
| 4-x |
| π |
| 2 |
则f(x)=4sinα+2cosα=2
| 5 |
根据三角函数图象,当α+arctan2=
| π |
| 2 |
| 5 |
当α=0时f(x)取得最小值2.
∴f(x)的值域为[2,2
| 5 |
故选:D.
点评:三角换元是一种十分实用的方法,它很好地体现了数学中一项基本的思想-转化.而且与许多知识都有交叉易错点换元后θ的范围十分重要,要根据具体的题目而定.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
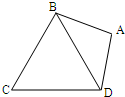 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=