Question

（本小题满分12分）

    已知f(x)是R上的奇函数，且当x＞0时，f(x)＝－x²＋2x＋2.

 (1)求f(x)的解析式；

 (2)画出f(x)的图象，并指出f(x)的单调区间．

 

Answer 1

【答案】

　(1) f(x)＝.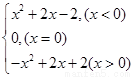

(2)其增区间为[－1,0)及(0,1]，减区间为(－∞，－1]及[1，＋∞)．

【解析】本试题主要是考查了函数的奇偶性和单调性的综合运用

（1）先根据已知条件，将函数设x＜0，则－x＞0，所以f(－x)＝－(－x)²－2x＋2＝－x²－2x＋2，得到解析式。

（2）画出函数的 图像。，结合图像的饿到函数的单调区间。

　(1)设x＜0，则－x＞0，所以f(－x)＝－(－x)²－2x＋2＝－x²－2x＋2，

又∵f(x)为奇函数，∴f(－x)＝－f(x)，∴f(x)＝x²＋2x－2，

又f(0)＝0，∴f(x)＝.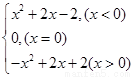

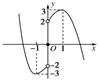
(2)先画出y＝f(x)(x＞0)的图象，利用奇函数的对称性可得到相应y＝f(x)(x＜0)的图象，其图象如图所示：由图可知，其增区间为[－1,0)及(0,1]，减区间为(－∞，－1]及[1，＋∞)．