Question

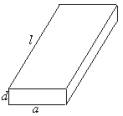
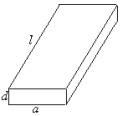
一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比．
（1）将此枕木翻转90°（即宽度变为了厚度），枕木的安全负荷变大吗？为什么？
（2）现有一根横断面为半圆（半圆的半径为R）的木材，用它来截取成长方体形的枕木，木材长度即为枕木规定的长度，问如何截取，可使安全负荷最大？

Answer 1

【答案】分析：（1）根据题意，可设原来的安全负荷为，将此枕木翻转90°后，枕木的宽度与厚度互换，安全负荷变为：．然后通过作商比较大小，讨论a、d的大小关系，可得正确结论；
（2）半圆的半径为R，设截取的枕木宽为a，高为d，则根据垂径定理，得a²+4d²=4R²．根据木材长度l为枕木规定的长度是一个不变的定值，得到当u=ad²最大时，安全负荷最大，建立关系式．利用基本不等式可得：当且仅当，u最大，即安全负荷达到最大值．
解答：解：（1）由题可设安全负荷为：（k为正常数），
则翻转90°后，安全负荷为：．
因为，
所以，当0＜d＜a时，y₁＜y₂．安全负荷变大；
当0＜a＜d时，y₁＞y₂，安全负荷变小．
（2）如图，设截取的枕木宽为a，高为d，
则根据垂径定理，得，即a²+4d²=4R²．

∵枕木长度不变，
∴u=ad²最大时，安全负荷最大
∴

当且仅当，
即取，时，u最大，即安全负荷最大．
点评：本题借助于一个实际问题，通过求枕木安全负荷的最值，着重考查了基本不等式在最值问题中的应用，考查了根据实际问题选择函数类型的方法，属于中档题．