题目内容
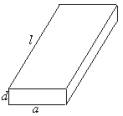
一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比,与它的厚度d的平方成正比,与它的长度l的平方成反比.
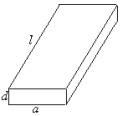
(1)将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷变大吗?为什么?
(2)现在一根横断面为半圆(半圆的半径为R)的木材,用它来截取成长方形的枕木,其长度即为枕木规定的长度,问如何截取,可使安全负荷最大?
答案:
解析:
解析:
答案:解:(1)安全负荷 ∵ ∴当0<d<a时,y1<y2,安全负荷变大; 当0<a<d时,y2<y1,安全负荷变小. (2)设截取的宽为a,高为d,则 ∵枕木长度不变, ∴u=ad2最大时,安全负荷最大. 当且仅当
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
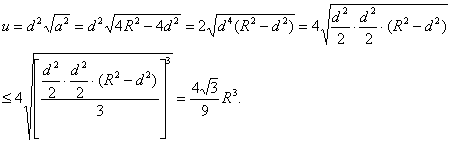
 一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比,与它的厚度d的平方成正比,与它的长度l的平方成反比.
一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比,与它的厚度d的平方成正比,与它的长度l的平方成反比.