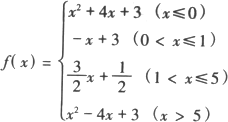题目内容

对于任意x∈R，函数f(x)表示－x＋3，x＋，x2－4x＋3中的较大者，则f(x)的最小值是________．

答案：2
解析：

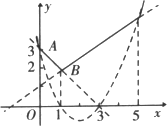
　　首先应理解题意，“函数f(x)表示－x＋3，x＋，x2－4x＋3中的较大者．”是指对某个区间而言，函数f(x)表示y＝－x＋3，y＝x＋，y＝x2－4x＋3中最大的一个．

　　其次是找出函数f(x)的表达式，此时可利用函数图象来确定．

　　如图所示，分别画出三个函数y＝－x＋3，y＝x＋，y＝x2－4x＋3的图象，得到三个交点A(0，3)，B(1，2)，C(5，8)．

　　从图象观察可得函数f(x)的表达式：

　　

　　f(x)的图象是图中的实线部分，图象的最低点是点B(1，2)，所以函数f(x)的最小值是3．


练习册系列答案
相关题目
对于任意x∈R，函数f（x）表示-x+3，
3
2
x+
1
2
，x2-4x+3中的较大者，则f（x）的最小值为（　　）
下列四种说法中，
①命题“存在x∈R，x2-x＞0”的否定是“对于任意x∈R，x2-x＜0”；
②；命题“p且q为真”是“p或q为真”的必要不充分条件；
③已知幂函数f（x）=xα的图象经过点（2，
2
2
），则f（4）的值等于
1
2

④某路公共汽车每7分钟发车一次，某位乘客到乘车点的时刻是随机的，则他候车时间超过3分钟的概率是
4
7
．
说法正确的序号是
③④
③④
．
下列说法中：
①函数f(x)=
x-1
x+1
与g（x）=x的图象没有公共点；
②若定义在R上的函数f（x）满足f（x+2）=-f（x-1），则6为函数f（x）的周期；
③若对于任意x∈（1，3），不等式x2-ax+2＜0恒成立，则a＞
11
3
；
④定义：“若函数f（x）对于任意x∈R，都存在正常数M，使|f（x）|≤M|x|恒成立，则称函数f（x）为有界泛函．”由该定义可知，函数f（x）=x2+1为有界泛函．
则其中正确的个数为
3
3
．

对于任意x∈R，函数f(x)表示－x＋3，，x2－4x＋3中的较大者，则f(x)的最小值是________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网