题目内容

对于任意x∈R，函数f（x）表示-x+3，
3
2
x+
1
2
，x2-4x+3中的较大者，则f（x）的最小值为（　　）
分析：分别作出三个函数的图象，利用数形结合求出f（x）的最小值．
解答：解：分别作出-x+3，
3
2
x+
1
2
，x2-4x+3的图象如图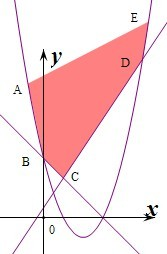：（阴影部分对应的曲线ABCDE），
则由图象可知函数f（x）在C处取得最小值，
由
y=-x+3
y=
3
2
x+
1
2
，得
x=1
y=2
，即（x）的最小值为2．
故选A．
点评：本题主要考查函数最值的判断，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
下列四种说法中，
①命题“存在x∈R，x2-x＞0”的否定是“对于任意x∈R，x2-x＜0”；
②；命题“p且q为真”是“p或q为真”的必要不充分条件；
③已知幂函数f（x）=xα的图象经过点（2，
2
2
），则f（4）的值等于
1
2

④某路公共汽车每7分钟发车一次，某位乘客到乘车点的时刻是随机的，则他候车时间超过3分钟的概率是
4
7
．
说法正确的序号是
③④
③④
．
下列说法中：
①函数f(x)=
x-1
x+1
与g（x）=x的图象没有公共点；
②若定义在R上的函数f（x）满足f（x+2）=-f（x-1），则6为函数f（x）的周期；
③若对于任意x∈（1，3），不等式x2-ax+2＜0恒成立，则a＞
11
3
；
④定义：“若函数f（x）对于任意x∈R，都存在正常数M，使|f（x）|≤M|x|恒成立，则称函数f（x）为有界泛函．”由该定义可知，函数f（x）=x2+1为有界泛函．
则其中正确的个数为
3
3
．

对于任意x∈R，函数f(x)表示－x＋3，，x2－4x＋3中的较大者，则f(x)的最小值是________．

对于任意x∈R，函数f(x)表示－x＋3，x＋，x2－4x＋3中的较大者，则f(x)的最小值是________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网