题目内容
下列四种说法中,
①命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x<0”;
②;命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2,
),则f(4)的值等于
④某路公共汽车每7分钟发车一次,某位乘客到乘车点的时刻是随机的,则他候车时间超过3分钟的概率是
.
说法正确的序号是
①命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x<0”;
②;命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2,
| ||
| 2 |
| 1 |
| 2 |
④某路公共汽车每7分钟发车一次,某位乘客到乘车点的时刻是随机的,则他候车时间超过3分钟的概率是
| 4 |
| 7 |
说法正确的序号是
③④
③④
.分析:命题①是考查特称命题的否定,特称命题的否定是全称命题;
命题②先由“p且q为真”推出p、q的真假,然后判断“p或q”的真假,反之再加以判断;
命题③直接把点的坐标代入幂函数求出α,然后在幂函数解析式中取x=4求值;
命题④是几何概型,注意测度比是时间比即可.
命题②先由“p且q为真”推出p、q的真假,然后判断“p或q”的真假,反之再加以判断;
命题③直接把点的坐标代入幂函数求出α,然后在幂函数解析式中取x=4求值;
命题④是几何概型,注意测度比是时间比即可.
解答:解:①命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x≤0”,故①不正确;
②命题“p且q为真”,则命题p、q均为真,所以“p或q为真”.反之“p或q为真”,则p、q不见得都真,所以不一定有“p且q为真”所以命题“p且q为真”是“p或q为真”的充分不必要条件,故命题②不正确;
③由幂函数f(x)=xα的图象经过点(2,
),所以2α=
,所以α=-
,所以幂函数为f(x)=x-
所以f(4)=4-
=
,所以命题③正确;
④由于公共汽车每7分钟发车一次,某位乘客到乘车点的时刻是随机的,该乘客在7分钟内的任意时刻都可能到达发车点,所以他候车时间超过3分钟的概率是
,故命题④正确.
故答案为③④.
②命题“p且q为真”,则命题p、q均为真,所以“p或q为真”.反之“p或q为真”,则p、q不见得都真,所以不一定有“p且q为真”所以命题“p且q为真”是“p或q为真”的充分不必要条件,故命题②不正确;
③由幂函数f(x)=xα的图象经过点(2,
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以f(4)=4-
| 1 |
| 2 |
| 1 |
| 2 |
④由于公共汽车每7分钟发车一次,某位乘客到乘车点的时刻是随机的,该乘客在7分钟内的任意时刻都可能到达发车点,所以他候车时间超过3分钟的概率是
| 4 |
| 7 |
故答案为③④.
点评:复合命题的真值表:



练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
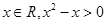 ”的否定是“对于任意
”的否定是“对于任意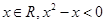 ”;
”;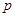 且
且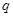 为真” 是“
为真” 是“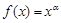 的图像经过点
的图像经过点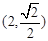 ,则
,则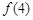 的值等于
的值等于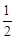
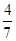 . 说法正确的序号是 .
. 说法正确的序号是 .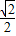 ),则f(4)的值等于
),则f(4)的值等于
 .
.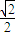 ),则f(4)的值等于
),则f(4)的值等于
 .
.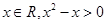 ”的否定是“对于任意
”的否定是“对于任意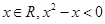 ”;
”;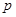 且
且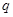 为真” 是“
为真” 是“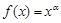 的图像经过点
的图像经过点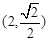 ,则
,则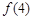 的值等于
的值等于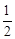
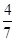 . 说法正确的序号是 .
. 说法正确的序号是 .