题目内容
下列四个命题中①“a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0”
②“k=1”是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件;
③“a=3”是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直”的充要条件;
④函数
 的最小值为2
的最小值为2其中假命题的为 将你认为是假命题的序号都填上)
【答案】分析:“全为0”的否定应该是“不全为0”,可得①是假命题;由三角函数的周期公式,得“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件是“k=±1”,得②是假命题;根据坐标系内两条直线垂直的表示式,可得③是假命题,根据基本不等式求取等号的条件,可得④的最小值2是取不到的,故④也是假命题.
解答:解:对于①,命题“a2+b2=0,则a,b全为0”的逆否命题是
“若a,b不全为0,则a2+b2≠0”,而不是“若a,b全不为0,则a2+b2≠0”,故①不正确;
对于②,函数y=cos2kx-sin2kx的最小正周期为π”的充要条件是“k=±1”,
故“k=1”不是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件,得②不正确;
对于③,当直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直时,3a+2(a-1)=0,解得a=
故“a=3”不是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直”的充要条件,得③不正确;
对于④,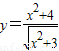 =
=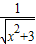 +
+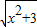 ,
,
虽然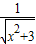 +
+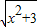 ≥2
≥2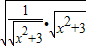 =2,
=2,
但是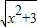
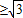 ,所以不等号的等号不能取到,故最小值不是2,故④不正确
,所以不等号的等号不能取到,故最小值不是2,故④不正确
故答案为:①②③④
点评:本题给出四个命题,要我们找出其中的假命题,着重考查了四种命题及其关系、三角函数的周期公式、坐标系内两条直线垂直的表示式和基本不等式求最值等知识,属于基础题.
解答:解:对于①,命题“a2+b2=0,则a,b全为0”的逆否命题是
“若a,b不全为0,则a2+b2≠0”,而不是“若a,b全不为0,则a2+b2≠0”,故①不正确;
对于②,函数y=cos2kx-sin2kx的最小正周期为π”的充要条件是“k=±1”,
故“k=1”不是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件,得②不正确;
对于③,当直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直时,3a+2(a-1)=0,解得a=

故“a=3”不是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直”的充要条件,得③不正确;
对于④,
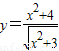 =
=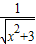 +
+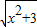 ,
,虽然
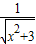 +
+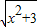 ≥2
≥2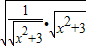 =2,
=2,但是
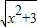
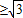 ,所以不等号的等号不能取到,故最小值不是2,故④不正确
,所以不等号的等号不能取到,故最小值不是2,故④不正确故答案为:①②③④
点评:本题给出四个命题,要我们找出其中的假命题,着重考查了四种命题及其关系、三角函数的周期公式、坐标系内两条直线垂直的表示式和基本不等式求最值等知识,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目