Question

平面α与β平行，且a?α，下列四个命题中
①a与β内的所有直线平行　　　　　
②a与β内的无数条直线平行
③a与β内的任意一条直线都不垂直　
④a与β无公共点
其中真命题的个数是

1. A.
   1
2. B.
   2
3. C.
   3
4. D.
   4

Answer 1

B
分析：因为α∥β，所以α与β无公共点，故α与β的直线可以平行或异面；若作一个平面与α、β都相交，则交线平行．据以上知识可判断出答案．
解答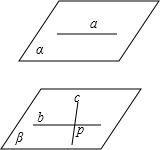：解：①如图所示：c?β，b?β，c∩b=P，b∥a，则a与c 是异面直线，故①不正确．
②b?β，则β内所有与b平行的直线皆与a平行，故②正确．
③若c⊥b，∵a∥b，∴a⊥c，故③不正确．
④∵α∥β，∴α与β无公共点，而a?α，∴a与β无公共点．故④正确．
综上可知：②④正确．
故选B．
点评：本题考查了两平行平面内的直线的位置关系，充分理解平行平面及性质和异面直线的定义是解决问题的关键．