题目内容
(本小题满分14分)
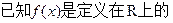 单调函数,
单调函数,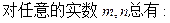
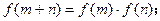
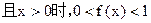 .
.
(1)证明:f(0)=1且x<0时f(x)>1;
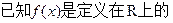 单调函数,
单调函数,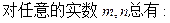
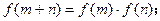
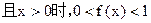 .
.(1)证明:f(0)=1且x<0时f(x)>1;
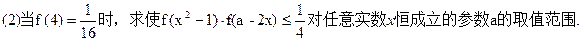 解:(1)在f(m+n)=f(m)·f(n)中,取m>0,n=0,有f(m)="f(m)·f(0) " ,
解:(1)在f(m+n)=f(m)·f(n)中,取m>0,n=0,有f(m)="f(m)·f(0) " ,∵x>0时0<f(x)<1 ∴f(0)="1 " ………3分
又设m=x<0,n="–x>0" 则0<f(–x)<1 ∴f(m+n)=" f(0)=" f(x)·f(–x)="1 "
∴f(x)=
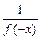 >1,即x<0时,f(x)>1………6分
>1,即x<0时,f(x)>1………6分(2)

∴f(x)是定义域R上的单调递减函数. ………8分
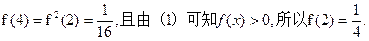 ………9分
………9分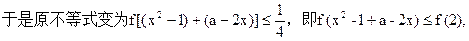 ………10分
………10分 …11分
…11分 ………14分
………14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ;
; 恒成立,试求a的取值范围.
恒成立,试求a的取值范围.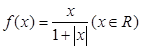 ,三位同学甲、乙、丙在研究此函数时给出命题:
,三位同学甲、乙、丙在研究此函数时给出命题: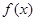 的值域为
的值域为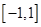 ;
;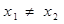 ,则一定有
,则一定有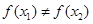 ;
;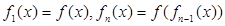 ,则
,则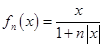 对任意
对任意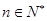 恒成立.
恒成立. ,则
,则 的值为( )
的值为( )
 9
9
 上的函数
上的函数 满足
满足 ,若
,若 且
且 ,则有( )
,则有( ) >
>

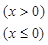 ,则
,则 的值是
的值是

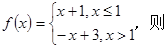 f(2) =
f(2) = 满足
满足 ="1" 且
="1" 且 ,则
,则 =_
=_ 若
若 ,则x=
,则x=