题目内容
 已知a=2(cosωx,cosωx),b=(cosωx,
已知a=2(cosωx,cosωx),b=(cosωx,| 3 |
| π |
| 3 |
(1)试求ω的值;
(2)先列表再作出函数f(x)在区间[-π,π]上的图象.
分析:(1)利用两个向量的数量积化简f(x)的解析式,由题意知,x=
时,函数f(x)取最值,故有
+
=kπ+
(k∈Z).
依据k、ω的范围求出它们的值.
(2)根据五点法作图的方法,分别令自变量x取-π、-
、-
、
、
、π,分别求出函数f(x)的值,
依据正弦函数的图象特点,在坐标系中描点作图.
| π |
| 3 |
| 2ωπ |
| 3 |
| π |
| 6 |
| π |
| 2 |
依据k、ω的范围求出它们的值.
(2)根据五点法作图的方法,分别令自变量x取-π、-
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
依据正弦函数的图象特点,在坐标系中描点作图.
解答:解:f(x)=
•
=2(cosωx,cosωx)•(cosωx,
sinωx)
=2cos2ωx+2
cosωxsinωx
=1+cos2ωx+
sin2ωx=1+2sin(2ωx+
).
(1)∵直线x=
为对称轴,∴sin(
+
)=±1,
∴
+
=kπ+
(k∈Z).
∴ω=
k+
,∵0<ω<1,
∴-
<k<
,∴k=0,ω=
.
(2)由(1)知,f(x)=1+2sin(x+
).
列表:
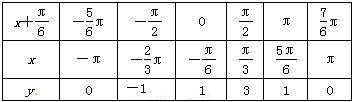
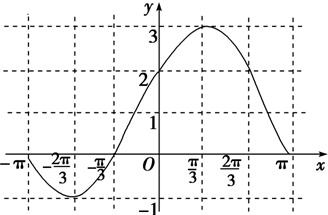
描点作图,函数f(x)在[-π,π]上的图象如图所示.
| a |
| b |
| 3 |
=2cos2ωx+2
| 3 |
=1+cos2ωx+
| 3 |
| π |
| 6 |
(1)∵直线x=
| π |
| 3 |
| 2ωπ |
| 3 |
| π |
| 6 |
∴
| 2ωπ |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴ω=
| 3 |
| 2 |
| 1 |
| 2 |
∴-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
(2)由(1)知,f(x)=1+2sin(x+
| π |
| 6 |
列表:

描点作图,函数f(x)在[-π,π]上的图象如图所示.

点评:本题考查两个向量的数量积公式的应用,两角和差的三角函数公式的应用,以及用五点法作y=Asin(ωx+φ)的图象.

练习册系列答案
相关题目
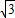 sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=
sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=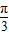 是函数f(x)图象的一条对称轴,
是函数f(x)图象的一条对称轴,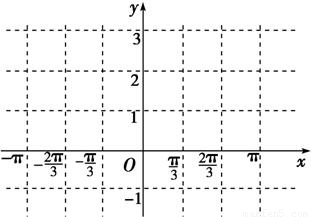
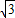 sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=
sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=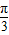 是函数f(x)图象的一条对称轴,
是函数f(x)图象的一条对称轴,