题目内容
设f(log2x)=2x(x>0),则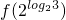 =
=
- A.128
- B.256
- C.512
- D.8
B
分析:设t=log2x则x=2t可先求得f(t)=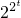 ,由于
,由于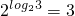 ,直接代入可求
,直接代入可求
解答:设t=log2x则x=2t
∴f(t)=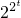
∵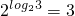
则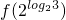 =f(3)=
=f(3)=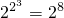 =256
=256
故选:B
点评:本题主要考查了利用换元法求解函数的解析式,对数的运算性质的应用及指数与对数的互化,属于基础性试题.
分析:设t=log2x则x=2t可先求得f(t)=
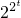 ,由于
,由于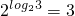 ,直接代入可求
,直接代入可求解答:设t=log2x则x=2t
∴f(t)=
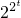
∵
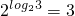
则
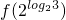 =f(3)=
=f(3)=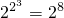 =256
=256故选:B
点评:本题主要考查了利用换元法求解函数的解析式,对数的运算性质的应用及指数与对数的互化,属于基础性试题.

练习册系列答案
相关题目