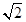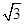题目内容
已知椭圆 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则该椭圆的离心率是( )
的焦点重合,则该椭圆的离心率是( )
A.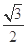 | B. | C. | D. |
D
解析

练习册系列答案
相关题目
设双曲线C: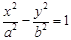 (
(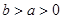 )的左、右焦点分别为 F1,F2.若在双曲线的右支上存在
)的左、右焦点分别为 F1,F2.若在双曲线的右支上存在
一点P,使得 |PF1|=3|PF2|,则双曲线C的离心率e的取值范围为 ( )
| A.(1,2) | B.(1,2] | C.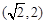 | D.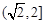 |
已知直线 被双曲线
被双曲线 的两条渐近线所截得线段的长度恰好等于其一个焦点到渐近线的距离,则此双曲线的离心率为( )
的两条渐近线所截得线段的长度恰好等于其一个焦点到渐近线的距离,则此双曲线的离心率为( )
A. | B. | C.2 | D.3 |
抛物线y=ax2的准线方程是y=2,则a的值为( )
A. | B.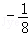 | C.8 | D.﹣8 |
已知直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,若椭圆的离心率为
两点,若椭圆的离心率为 ,焦距为2,则线段
,焦距为2,则线段 的长是( )
的长是( )
A. | B.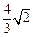 | C. | D. |
设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率取值范围是( )
A. | B.[-2,2] |
| C.[-1,1] | D.[-4,4] |
已知双曲线 的两条渐近线均与
的两条渐近线均与 相切,则该双曲线离心率等于( )
相切,则该双曲线离心率等于( )
A. | B. | C. | D. |
 上存在两个不同点处的切线重合,则称这条切线为曲线的自公切线,下列方程的曲线有自公切线的是( ).
上存在两个不同点处的切线重合,则称这条切线为曲线的自公切线,下列方程的曲线有自公切线的是( ).



 为C的实轴长的2倍,则C的离心率为
为C的实轴长的2倍,则C的离心率为