题目内容
若曲线 上存在两个不同点处的切线重合,则称这条切线为曲线的自公切线,下列方程的曲线有自公切线的是( ).
上存在两个不同点处的切线重合,则称这条切线为曲线的自公切线,下列方程的曲线有自公切线的是( ).
A. | B. |
C. | D. |
C
解析试题分析: 中曲线方程为
中曲线方程为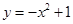 ,曲线是抛物线,没有自公切线,
,曲线是抛物线,没有自公切线,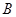 中方程化简为
中方程化简为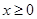 时,
时,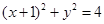 ,
,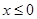 时,
时,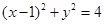 ,此曲线是两段劣圆弧,不存在自公切线,
,此曲线是两段劣圆弧,不存在自公切线, 中曲线如下图,是两个圆弧,相应的两个圆有公切线,即曲线有自公切线,选C.
中曲线如下图,是两个圆弧,相应的两个圆有公切线,即曲线有自公切线,选C.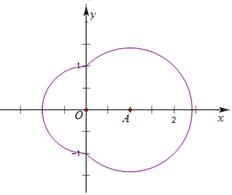
考点:方程与曲线,曲线的切线.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知点 在抛物线
在抛物线 上,且点
上,且点 到直线
到直线 的距离为
的距离为 ,则点
,则点 的个数为 ( )
的个数为 ( )
A. | B. | C.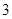 | D. |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B.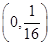 | C.(0,1) | D.(1,0) |
双曲线 的焦点坐标为( )
的焦点坐标为( )
A. , , | B. , , |
C. , , | D. , , |
已知椭圆 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则该椭圆的离心率是( )
的焦点重合,则该椭圆的离心率是( )
A.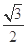 | B. | C. | D. |
直线 过抛物线
过抛物线 的焦点,且交抛物线于
的焦点,且交抛物线于 两点,交其准线于
两点,交其准线于 点,已知
点,已知 ,则
,则 ( )
( )
| A.2 | B. | C. | D.4 |
设圆锥曲线r的两个焦点分别为 ,若曲线r上存在点P满足
,若曲线r上存在点P满足 ,则曲线r的离心率等于( )
,则曲线r的离心率等于( )
A. 或 或 |
B. 或2 或2 |
C. 或2 或2 |
D. 或 或 |
 作垂直于实轴的弦
作垂直于实轴的弦 ,
, 是另一焦点,若∠
是另一焦点,若∠ ,则椭圆的离心率
,则椭圆的离心率 等于( )
等于( )



 的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( ) B.
B.
 D.
D.