题目内容
在极坐标系中,圆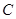 的极坐标方程为
的极坐标方程为 .现以极点
.现以极点 为原点,极轴为
为原点,极轴为 轴的非负半轴建立平面直角坐标系.
轴的非负半轴建立平面直角坐标系.
(Ⅰ)求圆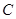 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若圆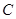 上的动点
上的动点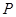 的直角坐标为
的直角坐标为 ,求
,求 的最大值,并写出
的最大值,并写出 取得最大值时点P的直角坐标.
取得最大值时点P的直角坐标.
(Ⅰ) ,即
,即 .
.
(Ⅱ) 取得最大值为
取得最大值为 ,P的直角坐标为
,P的直角坐标为 .
.
解析试题分析:(Ⅰ) ,两端同乘以
,两端同乘以 ,并将极坐标与直角坐标的互化公式代入即得.
,并将极坐标与直角坐标的互化公式代入即得.
(Ⅱ)将圆C的方程化为参数方程将 表示成三角函数式,确定得到
表示成三角函数式,确定得到 的最大值及点P的直角坐标.
的最大值及点P的直角坐标.
试题解析:(Ⅰ)由 ,得
,得 ,
,
所以圆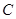 的直角坐标方程为
的直角坐标方程为 ,
,
即 . 3分
. 3分
(Ⅱ)由(Ⅰ)得圆C的参数方程为 (
( 为参数).
为参数).
所以 , 5分
, 5分
因此当 ,
, 时,
时, 取得最大值为
取得最大值为 ,
,
且当 取得最大值时点P的直角坐标为
取得最大值时点P的直角坐标为 . 7分
. 7分
考点:1、直角坐标方程与极坐标方程的互化,2、参数方程的应用,3、正弦型函数的性质.

练习册系列答案
相关题目
 .
.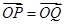 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程. 过点P(-2,-4)的直线
过点P(-2,-4)的直线 为参数)与曲线C相交于点M,N两点.
为参数)与曲线C相交于点M,N两点. 的普通方程;
的普通方程;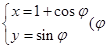 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.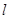 的极坐标方程是
的极坐标方程是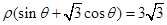 ,射线
,射线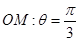 与圆C的交点为O,P,与直线
与圆C的交点为O,P,与直线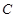 的圆心
的圆心 ,半径
,半径
 ,直线
,直线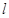 的参数方程为
的参数方程为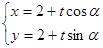 (
( 为参数),直线
为参数),直线 两点,求弦长
两点,求弦长 的取值范围
的取值范围 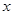 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为 ,直线的极坐标方程为
,直线的极坐标方程为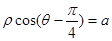 ,且点
,且点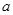 的值及直线的直角坐标方程;
的值及直线的直角坐标方程;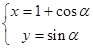 ,(
,(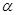 为参数),试判断直线与圆的位置关系.
为参数),试判断直线与圆的位置关系. 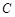 的极坐标方程是
的极坐标方程是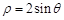 ,直线的参数方程是
,直线的参数方程是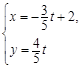 (为参数).
(为参数). 轴的交点是
轴的交点是 ,
, 是曲线
是曲线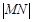 的最大值.
的最大值.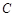 经过点
经过点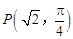 ,圆心为直线
,圆心为直线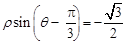 与极轴的交点,求圆
与极轴的交点,求圆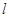 的极坐标方程为
的极坐标方程为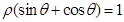 ,曲线
,曲线 的参数方程为
的参数方程为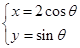 (
(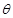 为参数).
为参数). ,求
,求 的面积.
的面积.