题目内容
函数 满足
满足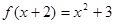 , 则
, 则 .
.
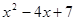
解析试题分析:设 ,所以
,所以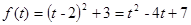 ,所以
,所以
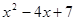 。
。
考点:函数解析式的求法。
点评:用换元法求函数的解析式,要注意新元的取值范围。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
题目内容
函数 满足
满足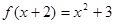 , 则
, 则 .
.
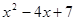
解析试题分析:设 ,所以
,所以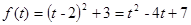 ,所以
,所以
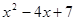 。
。
考点:函数解析式的求法。
点评:用换元法求函数的解析式,要注意新元的取值范围。

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案