题目内容
【题目】在平面
内，已知
，过直线
，
分别作平面
，
，使锐二面角
为
，锐二面角
为，则平面与平面所成的锐二面角的余弦值为（ ）.
A.
B.
C.
D.
【答案】A
【解析】
根据已知条件构造正四棱锥，可根据锐二面角
为
，锐二面角
为得出正四棱锥的高度.通过正四棱锥建立空间直角坐标系，用空间向量求平面
与平面
所成的锐二面角的余弦值.
如图
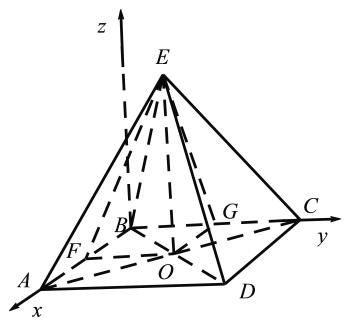
由题意以平面
为底面，以平面，为两相邻的侧面构造正四棱锥
，设正四棱锥的底面边长为2，以点
为坐标原点，以
，
，过点垂直于平面的直线分别为
轴、
轴、
轴建立空间直角坐标系，
在正四棱锥中设
，
为，中点，
，
则
，
，
∴
为二面角的平面角，
同理
为二面角的平面角，
∴
，
∴在
中，
，
则由题意易得
，
，
，
，
则
，
，
，
设平面的法向量为
，
则有
，
令
得平面的一个法向量为
，
同理可得平面的一个法向量为
，
则平面和平面所成锐二面角的余弦值为
.
故选:A.
天天向上口算本系列答案
【题目】在全面抗击新冠肺炎疫情这一特殊时期，我市教育局提出“停课不停学”的口号，鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系，对高三年级随机选取45名学生进行跟踪问卷，其中每周线上学习数学时间不少于5小时的有19人，余下的人中，在检测考试中数学平均成绩不少于120分的有10人，统计成绩后得到如下
列联表：
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | 10 | ||
合计 | 45 |
（1）请完成上面列联表；并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”；
（2）在上述样本中从分数不少于120分的学生中，按照分层抽样的方法，抽到线上学习时间不少于5小时和线上学习时间不足5小时的学生共5名，若在这5名学生中随机抽取2人，求至少1人每周线上学习时间不足5小时的概率.
（下面的临界值表供参考）
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式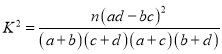
其中
）
【题目】2019年郑开国际马拉松比赛，于2019年3月31日在郑州、开封举行．某学校本着“我运动，我快乐，我锻炼，我提高”精神，积极组织学生参加比赛及相关活动，为了了解学生的参与情况，从全校学生中随机抽取了150名学生，对是否参与的情况进行了问卷调查，统计数据如下：
会参与 | 不会参与 | |
男生 | 60 | 40 |
女生 | 20 | 30 |
（1）根据上表说明，能否有97.5%的把握认为参与马拉松赛事与性别有关?
（2）现从参与问卷调查且参与赛事的学生中，采用按性别分层抽样的方法选取8人参加2019年马拉松比赛志愿者宣传活动，
①求男、女学生各选取多少人；
②若从这8人中随机选取2人到校广播站开展2019年赛事宣传介绍，求恰好选到2名男生的概率．
附：参考公式：
，其中
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
