题目内容
(本小题满分12分)
2011年深圳大运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D
两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假
设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某
运动员完成甲系列和乙系列的情况如下表:
甲系列:
|
动作 |
K |
D |
||
|
得分 |
100 |
80 |
40 |
10 |
|
概率 |
|
|
|
|
乙系列:
|
动作 |
K |
D |
||
|
得分 |
90 |
50 |
20 |
0 |
|
概率 |
|
|
|
|
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一
名的概率;
(II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
解:(I)若该运动员希望获得该项目的第一名,应选择甲系列.……1分
理由如下:选择甲系列最高得分为100+40=140>118,可能获得第一名;而选择乙系列最
高得分为90+20=110<118,不可能获得第一名. ……2分
记“该运动员完成K动作得100分”为事件A,“该运动员完成D动作得40分”为事件B,
则P (A)=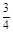 ,P (B)=
,P (B)=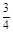 . …………4分
. …………4分
记“该运动员获得第一名”为事件C,依题意得
P
(C)=P (AB)+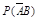 =
=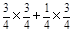 =
=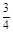 .
.
该运动员获得第一名的概率为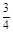 .…………6分
.…………6分
(II)若该运动员选择乙系列,X的可能取值是50,70,90,110, …………7分
则P (X=50)=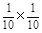 =
=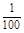 ,
,
P
(X=70)=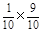 =
=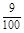 ,P (X=90)=
,P (X=90)=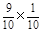 =
=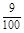 ,
,
P
(X=110)=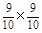 =
=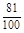 . …………9分
. …………9分
X的分布列为:
|
X |
50 |
70 |
90 |
110 |
|
P |
|
|
|
|
∴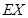 =50×
=50×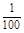 +70×
+70×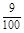 +90×
+90×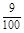 +110×
+110×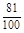 =104. ……12分
=104. ……12分
【解析】略

 习题精选系列答案
习题精选系列答案


