题目内容
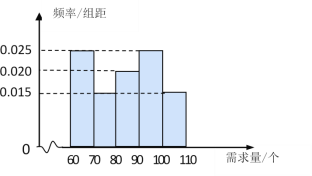
【题目】从某校高中男生中随机选取100名学生，将他们的体重（单位： 
）数据绘制成频率分布直方图，如图所示．
（1）估计该校的100名同学的平均体重（同一组数据以该组区间的中点值作代表）；
（2）若要从体重在
， 
， 
三组内的男生中，用分层抽样的方法选取6人组成一个活动队，再从这6人中选2人当正副队长，求这2人中至少有1人体重在
内的概率．
【答案】（1）
（2）
【解析】试题分析：（1）每个小矩形的中点横坐标与纵坐标的积之和就是该校的
名同学的平均体重；（2）记体重在
的
人为
， 
， 
， 
的
人为
， 
， 
的1人为
，利用列举法求出总事件个数为
种，符合条件的事件个数为
，利用古典概型概率公式可得结果.
试题解析：（1）估计该校的100名同学的平均体重为：
．
（2）由频率分布直方图可知体重在
， 
， 
三组内的男生人数分别为
， 
， 
，
故这三组中通过分层抽样所抽取的人数分别为3,2,1．
记体重在
的3人为
， 
， 
， 
的2人为
， 
， 
的1人为
，
则从这6人中抽取2人的所有可能结果为： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
共15种，
其中体重在
至少有1人的结果有： 
， 
， 
， 
， 
， 
， 
， 
， 
共9种，故这2人中至少有1人体重在
内的概率为
．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】为调查银川市某校高中生是否愿意提供志愿者服务，用简单随机抽样方法从该校调查了50人，结果如下：
（1）用分层抽样的方法在愿意提供志愿者服务的学生中抽取6人，其中男生抽取多少人？
（2）在（1）中抽取的6人中任选2人，求恰有一名女生的概率；
（3）你能否在犯错误的概率不超过0.010的前提下，认为该校高中生是否愿意提供志愿者服务与性别有关？
下面的临界值表供参考：
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
独立性检验统计量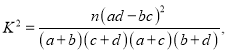
其中
【题目】某化工厂为预测产品的回收率
，需要研究它和原料有效成分含量
之间的相关关系，现收集了4组对照数据。
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
（Ⅰ）请根据相关系数
的大小判断回收率
与
之间是否存在高度线性相关关系；
（Ⅱ）请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程
，并预测当
时回收率
的值.
参考数据： 
| 1 | 0 |
|
| 其他 |
| 完全相关 | 不相关 | 高度相关 | 低度相关 | 中度相关 |
， 
