题目内容
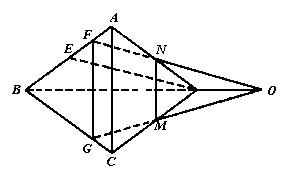
已知空间四边形ABCD的各个边长和对角线长都是a,DE是DABD中AB边上的高,F为AE中点,过F有一平面和AC、DE都平行.
(1)求该平面与空间四边形各边截得各点组成的四边形FGMN的面积;
(2)求证:BD与截面和空间四边形ABCD中的两个面ABD、BCD的交线共点
答案:
解析:
解析:
(1)解: (2)证明:设FN∩GM=O,由FNÌ平面ABC,GMÌ平面BCD,即证.
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点,求证:
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点,求证:
