题目内容
 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.求证:
(1)AB⊥平面CDE;
(2)平面CDE⊥平面ABC;
(3)若G为△ADC的重心,试在线段AE上确定一点F,使得GF∥平面CDE.
分析:(1)要证明AB⊥平面CDE,只需证明AB垂直平面CDE内的两条相交直线CE、DE即可;
(2)易证AB⊥平面CDE,就能证明平面CDE⊥平面ABC;
(3)G为△ADC的重心,连接AG并延长交CD于H,连接EH,推出GF∥EH,AF=2FE可得GF∥平面CDE.
(2)易证AB⊥平面CDE,就能证明平面CDE⊥平面ABC;
(3)G为△ADC的重心,连接AG并延长交CD于H,连接EH,推出GF∥EH,AF=2FE可得GF∥平面CDE.
解答: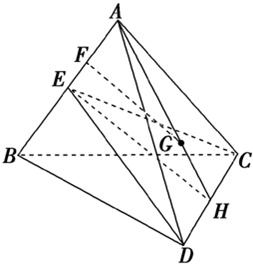 证明:(1)
证明:(1)
?CE⊥AB,同理,
?DE⊥AB,
又∵CE∩DE=E,∴AB⊥平面CDE.
(2)由(1)知AB⊥平面CDE,
又∵AB?平面ABC,
∴平面CDE⊥平面ABC.
(3)连接AG并延长交CD于H,连接EH,则
=
,
在AE上取点F使得
=
,
则GF∥EH,
易知当AF=2FE时,GF∥平面CDE.
 证明:(1)
证明:(1)
|
|
又∵CE∩DE=E,∴AB⊥平面CDE.
(2)由(1)知AB⊥平面CDE,
又∵AB?平面ABC,
∴平面CDE⊥平面ABC.
(3)连接AG并延长交CD于H,连接EH,则
| AG |
| GH |
| 2 |
| 1 |
在AE上取点F使得
| AF |
| FE |
| 2 |
| 1 |
则GF∥EH,
易知当AF=2FE时,GF∥平面CDE.
点评:本题考查直线与平面垂直的判定,直线与平面平行,考查逻辑思维能力,空间想象能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知空间四边形ABCD中,
如图,已知空间四边形ABCD中, 如图,已知空间四边形ABCD的对角线AC=10,BD=6,M、N分别是AB、CD的中点,MN=7,求异面直线AC与BD所成的角.
如图,已知空间四边形ABCD的对角线AC=10,BD=6,M、N分别是AB、CD的中点,MN=7,求异面直线AC与BD所成的角. 如图,已知空间四边形ABCD中,AB=CD=3,E、F分别是BC、AD上的点,并且BE:EC=AF:FD=1:2,EF=
如图,已知空间四边形ABCD中,AB=CD=3,E、F分别是BC、AD上的点,并且BE:EC=AF:FD=1:2,EF= 如图,已知空间四边形ABCD中,O是对角线BD的中点,
如图,已知空间四边形ABCD中,O是对角线BD的中点,