题目内容
13.(1)化简$\frac{{\sqrt{1-2sin10°cos10°}}}{{sin170°-\sqrt{1-{{sin}^2}170°}}}$;(2)已知tan α=-$\frac{1}{2}$,求$\frac{2sinα•cosα}{sin2α-cos2α}$.分析 (1)由诱导公式及同角三角函数关系式即可化简求值.
(2)利用倍角公式及万能公式化简所求即可得解.
解答 解:(1)$\frac{{\sqrt{1-2sin10°cos10°}}}{{sin170°-\sqrt{1-{{sin}^2}170°}}}$=$\frac{\sqrt{(cos10°-sin10°)^{2}}}{sin10°-cos10°}$=$\frac{cos10°-sin10°}{-(cos10°-sin10°)}$=-1.
(2)∵tanα=-$\frac{1}{2}$,
∴$\frac{2sinα•cosα}{sin2α-cos2α}$=$\frac{sin2α}{sin2α-cos2α}$=$\frac{\frac{2tanα}{1+ta{n}^{2}α}}{\frac{2tanα}{1+ta{n}^{2}α}-\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}}$=$\frac{\frac{2×(-\frac{1}{2})}{1+\frac{1}{4}}}{\frac{2×(-\frac{1}{2})}{1+\frac{1}{4}}-\frac{1-\frac{1}{4}}{1+\frac{1}{4}}}$=$\frac{4}{7}$.
点评 本题主要考查了同角三角函数基本关系的运用,考查了诱导公式,万能公式,二倍角公式的应用,属于基本知识的考查.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8.若|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
2.各项均为实数的等比数列{an}中,a1=1,a3=2,则a5=( )
| A. | 4 | B. | $\sqrt{2}$ | C. | ±4 | D. | ±$\sqrt{2}$ |
3.函数值tan224°,sin136°,cos310°的大小关系是( )
| A. | cos310°<sin136°<tan224° | B. | sin136°<cos310°<tan224° | ||
| C. | cos310°<tan224°<sin136° | D. | tan224°<sin136°<cos310° |
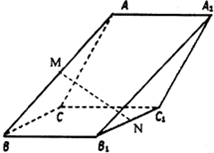 如图,在斜三棱柱ABCD-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠B1C1C=∠C1CA=60°,AC=2,其中M,N分别是AB,B1C1的中点,
如图,在斜三棱柱ABCD-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠B1C1C=∠C1CA=60°,AC=2,其中M,N分别是AB,B1C1的中点,