题目内容
8.已知△ABC中,b2+c2>a2,且角A为三个内角中的最大角,则角A的取值范围是 ( )| A. | (120°,180°) | B. | (90°,120°) | C. | (60°,90°) | D. | (45°,60°) |
分析 利用三角形的内角和以及余弦定理求出A的范围即可.
解答 解:△ABC中,b2+c2>a2,且角A为三个内角中的最大角,
可得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$>0,可得A∈(0°,90°),
A+B+C=180°,可得180°<3A,则A>60°.
∴A∈(60°,90°).
故选:C.
点评 本题考查余弦定理以及三角形的解法,考查计算能力.

练习册系列答案
相关题目
16.已知集合A={x|x2-2x-3<0},B={x|lnx>0},则A∩B=( )
| A. | {x|x>1} | B. | {x|x<3} | C. | {x|1<x<3} | D. | {x|-1<x<1} |
18.下列各组中的函数图象相同的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=1,g(x)=$\frac{x}{x}$ | ||
| C. | f(x)=$\frac{(x+3)^{2}}{x+3}$,g(x)=(x+3)(x+3)0 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,x>0}\\{-x,x<0}\end{array}\right.$ |
 如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上的一点.
如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上的一点.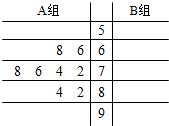 某班A、B两组各有8名学生,他们期中考试的美术成绩如下:
某班A、B两组各有8名学生,他们期中考试的美术成绩如下: