题目内容
已知向量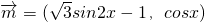 ,
,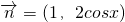 设函数
设函数 .
.
(1)求函数f(x)的最大值和最小正周期;
(2)求函数f(x)的单调增区间和图象的对称轴方程.
解: =
= sin2x-1+2cos2x=
sin2x-1+2cos2x= sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+ )
)
(1)由于函数 =2sin(2x+
=2sin(2x+ ),所以函数的周期是:T=
),所以函数的周期是:T= ,函数的最大值为:2.
,函数的最大值为:2.
(2)因为2x+ ∈[-
∈[-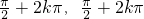 ]k∈Z 解得:x∈[
]k∈Z 解得:x∈[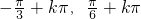 ]k∈Z就是函数的单调增区间.
]k∈Z就是函数的单调增区间.
函数图象的对称轴方程为:x=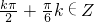
分析:化简函数 .为2sin(2x+
.为2sin(2x+ )
)
(1)利用正弦函数的有界性,直接求函数f(x)的最大值,求出最小正周期;
(2)利用正弦函数的单调增区间,求函数f(x)的单调增区间,正弦函数的对称轴方程求函数的对称轴方程.
点评:本题考查正弦函数的单调性,三角函数的周期性及其求法,正弦函数的对称性,复合三角函数的单调性,考查计算能力,正弦函数的基本性质,是基础题,利用向量的数量积及其化简三角函数,是解题的基础.
 =
= sin2x-1+2cos2x=
sin2x-1+2cos2x= sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+ )
)(1)由于函数
 =2sin(2x+
=2sin(2x+ ),所以函数的周期是:T=
),所以函数的周期是:T= ,函数的最大值为:2.
,函数的最大值为:2.(2)因为2x+
 ∈[-
∈[-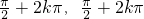 ]k∈Z 解得:x∈[
]k∈Z 解得:x∈[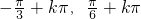 ]k∈Z就是函数的单调增区间.
]k∈Z就是函数的单调增区间.函数图象的对称轴方程为:x=
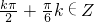
分析:化简函数
 .为2sin(2x+
.为2sin(2x+ )
)(1)利用正弦函数的有界性,直接求函数f(x)的最大值,求出最小正周期;
(2)利用正弦函数的单调增区间,求函数f(x)的单调增区间,正弦函数的对称轴方程求函数的对称轴方程.
点评:本题考查正弦函数的单调性,三角函数的周期性及其求法,正弦函数的对称性,复合三角函数的单调性,考查计算能力,正弦函数的基本性质,是基础题,利用向量的数量积及其化简三角函数,是解题的基础.

练习册系列答案
相关题目

 ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中常数
对称,其中常数
 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 的图像.
的图像. ,设函数
,设函数 ;
; 求函数f(x)的最值及对应的x的值;-
求函数f(x)的最值及对应的x的值;- 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. ,设函数
,设函数 .
. ,求f(A+B)的值.
,求f(A+B)的值. ,
, 设函数
设函数 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,
, ,求
,求 的最大值.
的最大值.