题目内容
已知向量 ,设函数
,设函数 .
.(1)求函数f(x)的值域;
(2)已知锐角△ABC的三个内角分别为A,B,C,若
 ,求f(A+B)的值.
,求f(A+B)的值.
【答案】分析:(1)根据所给的两个向量的坐标,写出函数f(x)的解析式,逆用正弦的二倍角公式,把函数变形为y=sinx的形式,根据所给的变量的取值范围,写出函数的值域.
(2)根据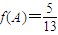 ,
,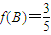 ,写出三角形的两个内角的三角函数值,根据三角形是锐角三角形和同角的三角函数关系,根据两角和的正弦公式,得到结果.
,写出三角形的两个内角的三角函数值,根据三角形是锐角三角形和同角的三角函数关系,根据两角和的正弦公式,得到结果.
解答:解:(1)∵向量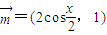 ,
,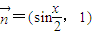 (x∈R),
(x∈R),
∴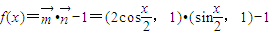
=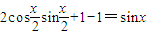 .
.
∵x∈R,
∴函数f(x)的值域为[-1,1].
(2)∵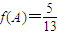 ,
,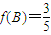 ,∴
,∴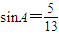 ,
,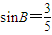 .
.
∵A,B都是锐角,
∴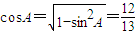 ,
,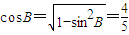 .
.
∴f(A+B)=sin(A+B)=sinAcosB+cosAsinB
=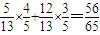 .
.
∴f(A+B)的值为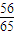 .
.
点评:本题表面上是对向量数量积的考查,根据两个向量的坐标,用数量积列出式子,但是这步工作做完以后,题目的重心转移到角的变换问题.注意解题过程中角的范围.
(2)根据
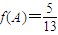 ,
,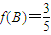 ,写出三角形的两个内角的三角函数值,根据三角形是锐角三角形和同角的三角函数关系,根据两角和的正弦公式,得到结果.
,写出三角形的两个内角的三角函数值,根据三角形是锐角三角形和同角的三角函数关系,根据两角和的正弦公式,得到结果.解答:解:(1)∵向量
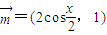 ,
,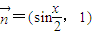 (x∈R),
(x∈R),∴
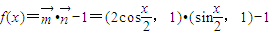
=
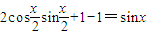 .
.∵x∈R,
∴函数f(x)的值域为[-1,1].
(2)∵
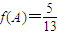 ,
,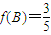 ,∴
,∴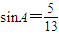 ,
,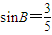 .
.∵A,B都是锐角,
∴
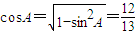 ,
,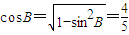 .
.∴f(A+B)=sin(A+B)=sinAcosB+cosAsinB
=
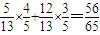 .
.∴f(A+B)的值为
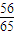 .
.点评:本题表面上是对向量数量积的考查,根据两个向量的坐标,用数量积列出式子,但是这步工作做完以后,题目的重心转移到角的变换问题.注意解题过程中角的范围.

练习册系列答案
相关题目

 ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中常数
对称,其中常数
 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 的图像.
的图像. ,设函数
,设函数 ;
; 求函数f(x)的最值及对应的x的值;-
求函数f(x)的最值及对应的x的值;- 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. ,
, 设函数
设函数 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,
, ,求
,求 的最大值.
的最大值.