题目内容
已知△ABC的三边a、b、c成等比数列,且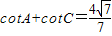 ,a+c=3.
,a+c=3.(1)求cosB;(2)求△ABC的面积.
【答案】分析:(1)由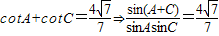 ,由sinAsinC=sin2B,sin(A+C)=sinB,知
,由sinAsinC=sin2B,sin(A+C)=sinB,知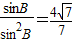 ,
,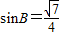 ,由此能求出cosB.
,由此能求出cosB.
(2)由余弦定理 b2=a2+c2-2accosB,得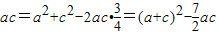 ,由此能求出△ABC的面积.
,由此能求出△ABC的面积.
解答:解:(1)由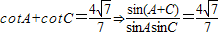 ,
,
∵sinAsinC=sin2B,
sin(A+C)=sinB,
∴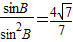
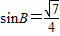 ,…(5分)
,…(5分)
由a、b、c成等比数列,
知b2=ac,
且b不是最大边,
∴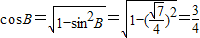 ,…(6分)
,…(6分)
(2)由余弦定理 b2=a2+c2-2accosB,
得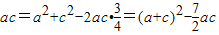 ,
,
得ac=2,…(11分)
∴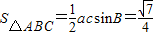 .…(12分)
.…(12分)
点评:本题考查三角形的解法,解题时要认真审题,仔细解答,注意正弦定理和余弦定理的灵活运用.
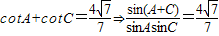 ,由sinAsinC=sin2B,sin(A+C)=sinB,知
,由sinAsinC=sin2B,sin(A+C)=sinB,知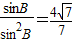 ,
,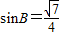 ,由此能求出cosB.
,由此能求出cosB.(2)由余弦定理 b2=a2+c2-2accosB,得
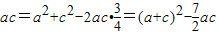 ,由此能求出△ABC的面积.
,由此能求出△ABC的面积.解答:解:(1)由
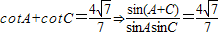 ,
,∵sinAsinC=sin2B,
sin(A+C)=sinB,
∴
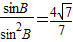
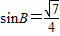 ,…(5分)
,…(5分)由a、b、c成等比数列,
知b2=ac,
且b不是最大边,
∴
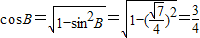 ,…(6分)
,…(6分)(2)由余弦定理 b2=a2+c2-2accosB,
得
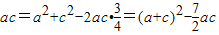 ,
,得ac=2,…(11分)
∴
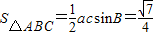 .…(12分)
.…(12分)点评:本题考查三角形的解法,解题时要认真审题,仔细解答,注意正弦定理和余弦定理的灵活运用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
已知△ABC的三边a、b、c的长均为正整数,且a≤b≤c,若b为常数,则满足要求的△ABC的个数是( )
| A、b2 | ||||
B、
| ||||
C、
| ||||
D、
|