题目内容
【题目】阿波罗尼斯（古希腊数学家，约公元前262-190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，它将圆锥曲线的性质网罗殆尽，几乎使后人没有插足的余地.他证明过这样一个命题：平面内与两定点距离的比为常数
的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.①若定点为
，写出
的一个阿波罗尼斯圆的标准方程__________；②△
中，
，则当△面积的最大值为
时，
______.
【答案】
【解析】
（1）设动点为
，则
或
，化简即得阿波罗尼斯圆的标准方程；
（2）设
，
，得到点
的轨迹方程是
，再求出圆的半径为
，解方程
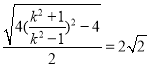即得解.
（1）设动点为，则或，
所以
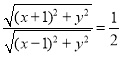或
，
化简得.
所以
的一个阿波罗尼斯圆的标准方程为.
（2）设，，
因为
，
所以
，
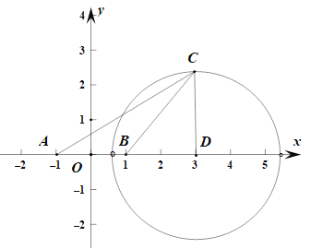
所以，点的轨迹是图中的圆
.
当△
面积的最大值为时，
轴，此时
就是圆的半径，
所以圆的半径为.
所以
.
故答案为：；.
练习册系列答案
相关题目
