题目内容
【题目】家具公司制作木质的书桌和椅子，需要木工和漆工两道工序，已知木工平均四个小时做一把椅子，八个小时做一张书桌，该公司每星期木工最多有8000个工作时；漆工平均两小时漆一把椅子、一小时漆一张书桌，该公司每星期漆工最多有1300个工作时，又已知制作一把椅子和一张书桌的利润分别是15元和20元，试根据以上条件，问怎样安排生产能获得最大利润?
【答案】安排生产200把椅子，900张桌子时，利润最大为21000元.
【解析】
先设每天生产桌子x张，椅子y张，利润总额为P千元，根据题意抽象出x，y满足的条件，建立约束条件，作出可行域，再根据目标函数P═15x+20y，利用截距模型，平移直线找到最优解，即可．
解：设每天生产桌子x张，椅子y张，利润总额为p，目标函数为：p＝15x+20y
则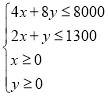
作出可行域：
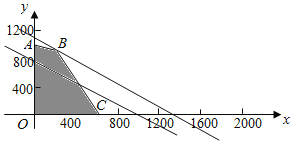
把直线l：3x+4y＝0向右上方平移至l'的位置时，直线经过可行域上的点B，此时p＝15x+20y取最大值，
解方程
得B的坐标为（200，900）．
p＝15×200+20×900＝21000．
答：每天应生产桌子200张，椅子900张才能获得最大利润．
练习册系列答案
相关题目
