题目内容
满足条件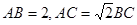 的三角形
的三角形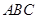 的面积的最大值为 .
的面积的最大值为 .
【答案】
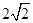
【解析】解:设BC=x,则AC= 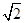 x,
x,
根据面积公式得S△ABC=1 /2 AB•BCsinB
=1/ 2 ×2x 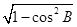 ,
,
根据余弦定理得cosB=(AB2+BC2-AC2)/2AB•BC=[4+x2-( 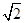 x)2] /4x =(4-x2) /4x ,
x)2] /4x =(4-x2) /4x ,
代入上式得
S△ABC=x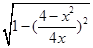
由三角形三边关系有 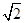 x+x>2
x+x>2
x+2>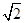 x ,
x ,
解得2 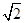 -2<x<2
-2<x<2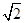 +2.
+2.
故当x=2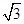 时,S△ABC取得最大值2
时,S△ABC取得最大值2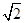

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
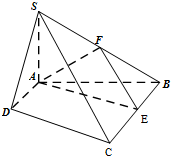 如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,且BC=2AD=2,AB=4,SA=3.
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,且BC=2AD=2,AB=4,SA=3. 一块边长为10的正方形纸片,按如图所示将阴影部分裁下,然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD(底面是正方形,顶点在底面的射影是底面中心的四棱锥).
一块边长为10的正方形纸片,按如图所示将阴影部分裁下,然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD(底面是正方形,顶点在底面的射影是底面中心的四棱锥).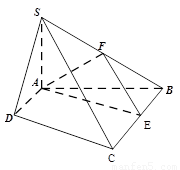
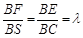 .(
.(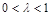 )
)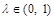 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;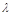 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的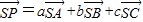 (a+b+c=1),在第(1)问的条件下,求
(a+b+c=1),在第(1)问的条件下,求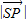 的最小值,并求取得最小值时a,b,c的值;
的最小值,并求取得最小值时a,b,c的值;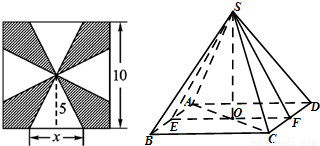
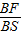 =
=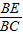 =λ.(0<λ<1)
=λ.(0<λ<1)