题目内容
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,且BC=2AD=2,AB=4,SA=3.(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足
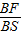 =
=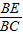 =λ.(0<λ<1)
=λ.(0<λ<1)①求证:对于任意的λ∈(0,1),恒有SC∥平面AEF;
②是否存在λ,使得△AEF为直角三角形,若存在,求出所有符合条件的λ值;若不存在,说明理由.

【答案】分析:(1)通过平面SAB内的直线BC垂直平面SAB,利用平面与平面垂直的判定定理证明:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足 =
= =λ.(0<λ<1)
=λ.(0<λ<1)
①直接利用直线与平面平行,判断对于任意的λ∈(0,1),恒有SC∥平面AEF;
②存在λ,使得△AEF为直角三角形,分别通过三角形的三个角为90°,通过直线与平面垂直,求出满足题意的λ值,或推出矛盾的结果,即可说明存在λ.
解答: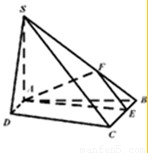 证明:(1)∵SA⊥平面ABCD,∴SA⊥BC,
证明:(1)∵SA⊥平面ABCD,∴SA⊥BC,
∵底面ABCD为直角梯形,AD∥BC,∠BAD=90°,∴BC⊥AB,
∵SA∩AB=A,∴BC⊥平面SAB,
∵BC?平面SAB,∴平面SBC⊥平面SAB;
(2)①∵ ,∴EF∥SC,
,∴EF∥SC,
∵SC?平面AEF,EF?平面AEF,
∴对任意的λ∈(0,1),恒有SC∥平面AEF.
②存在λ,使得△AEF为直角三角形,
1°:若∠AFE=90°,即AF⊥EF,由(1)可知,BC⊥平面SAB,
∵AF?平面SAB,∴BC⊥AF,
∵EF∩BC=E,EF?平面SBC,∴AF⊥平面SBC,∴AF⊥BS,
在Rt△SAB中,AB=4,SA=3,∴BS=5,∴SF=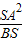 =
= ,
,
∴FB=5-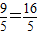 ,
, .
.
2°:若∠FAE=90°,AF⊥AE,由1°:可知,BC⊥AF,
∵BC∩AE=E,AE?平面ABCD,∴AF⊥平面ABCD,
又因为SA⊥平面ABCD,这与够一点有且只有一条直线与已知平面垂直相矛盾,
∴∠FAE≠90°.
3°:若∠AEF=90°,即AE⊥EF,由(1)可知,E∥SC,∴AE⊥SC,
又∵SA⊥平面ABCD,AE?平面ABCD,∴AE⊥SA,SA∩SC=S,
∴AE⊥平面SAC,∴AE⊥AC,
这与∠BAD=90°矛盾,
所以∠AEF≠90°.
综上当且仅当 ,使得△AEF为直角三角形.
,使得△AEF为直角三角形.
点评:本题考查平面与平面垂直的判定定理的应用,直线与平面平行与垂直的判定定理的应用,考查空间想象能力,逻辑推理能力,分类讨论思想的应用.
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足
 =
= =λ.(0<λ<1)
=λ.(0<λ<1)①直接利用直线与平面平行,判断对于任意的λ∈(0,1),恒有SC∥平面AEF;
②存在λ,使得△AEF为直角三角形,分别通过三角形的三个角为90°,通过直线与平面垂直,求出满足题意的λ值,或推出矛盾的结果,即可说明存在λ.
解答:
 证明:(1)∵SA⊥平面ABCD,∴SA⊥BC,
证明:(1)∵SA⊥平面ABCD,∴SA⊥BC,∵底面ABCD为直角梯形,AD∥BC,∠BAD=90°,∴BC⊥AB,
∵SA∩AB=A,∴BC⊥平面SAB,
∵BC?平面SAB,∴平面SBC⊥平面SAB;
(2)①∵
 ,∴EF∥SC,
,∴EF∥SC,∵SC?平面AEF,EF?平面AEF,
∴对任意的λ∈(0,1),恒有SC∥平面AEF.
②存在λ,使得△AEF为直角三角形,
1°:若∠AFE=90°,即AF⊥EF,由(1)可知,BC⊥平面SAB,
∵AF?平面SAB,∴BC⊥AF,
∵EF∩BC=E,EF?平面SBC,∴AF⊥平面SBC,∴AF⊥BS,
在Rt△SAB中,AB=4,SA=3,∴BS=5,∴SF=
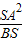 =
= ,
,∴FB=5-
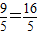 ,
, .
.2°:若∠FAE=90°,AF⊥AE,由1°:可知,BC⊥AF,
∵BC∩AE=E,AE?平面ABCD,∴AF⊥平面ABCD,
又因为SA⊥平面ABCD,这与够一点有且只有一条直线与已知平面垂直相矛盾,
∴∠FAE≠90°.
3°:若∠AEF=90°,即AE⊥EF,由(1)可知,E∥SC,∴AE⊥SC,
又∵SA⊥平面ABCD,AE?平面ABCD,∴AE⊥SA,SA∩SC=S,
∴AE⊥平面SAC,∴AE⊥AC,
这与∠BAD=90°矛盾,
所以∠AEF≠90°.
综上当且仅当
 ,使得△AEF为直角三角形.
,使得△AEF为直角三角形.点评:本题考查平面与平面垂直的判定定理的应用,直线与平面平行与垂直的判定定理的应用,考查空间想象能力,逻辑推理能力,分类讨论思想的应用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC. 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB= (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2. (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.