题目内容
设某大学的女生体重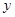 (单位:
(单位: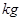 )与身高
)与身高 (单位:
(单位: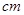 )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据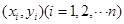 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为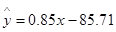 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.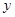 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心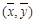 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
D.
解析试题分析:根据回归方程为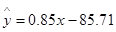 知,
知,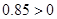 ,所以
,所以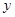 与
与 具有正的线性相关关系,故
具有正的线性相关关系,故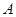 正确;又因为回归直线过样本点的中心
正确;又因为回归直线过样本点的中心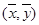 ,故
,故 正确;因为
正确;因为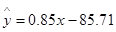 ,所以该大学某女生身高增加lcm,则其体重约增加0.85kg,故
,所以该大学某女生身高增加lcm,则其体重约增加0.85kg,故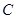 正确;当
正确;当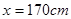 时,
时,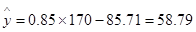 ,但这是预测值,不可断定其体重为58.79kg,故
,但这是预测值,不可断定其体重为58.79kg,故 不正确.
不正确.
考点:回归分析的初步应用.

练习册系列答案
相关题目
某初级中学领导采用系统抽样方法,从该校800名学生中抽50名学生做牙齿健康检查.现将800名学生从1到800进行编号,求得间隔数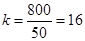 ,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( )
,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( )
| A.39 | B.40 | C.37 | D.38 |
下列说法中,正确的是( )
| A.频率分布直方图中各小长方形的面积不等于相应各组的频率; |
| B.一组数据的标准差是这组数据的方差的平方; |
| C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半; |
| D.一组数据的方差越大,说明这组数据的波动越大. |
两个变量 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1的相关指数 为0.98 为0.98 | B.模型2的相关指数 为0.86 为0.86 |
C.模型3的相关指数 为0.68 为0.68 | D.模型4的相关指数 为0.58 为0.58 |
我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为( )
| A.45,75,15 | B.45,45,45 | C.30,90,15 | D.45,60,30 |
(5分)(2011•陕西)设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n次方个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论正确的是( )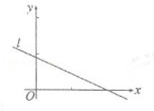
A.直线l过点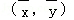 |
| B.x和y的相关系数为直线l的斜率 |
| C.x和y的相关系数在0到1之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
 ,
,  B.
B. C.
C. ,
,
 位员工的月工资(单位:元)为
位员工的月工资(单位:元)为 ,
, ,…,
,…, ,其均值和方差分别为
,其均值和方差分别为 和
和 ,若从下月起每位员工的月工资增加
,若从下月起每位员工的月工资增加 元,则这
元,则这
 ,
,