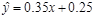题目内容
对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图如图,则估计此样本的众数、中位数分别为( ) ,
,  B.
B. ,
, C.
C. ,
, D.
D. ,
, 

B
解析试题分析:由图可知,前五组的频率依次为: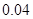 ,
,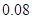 ,
,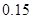 ,
,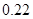 ,
,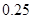 ,因此前五组的频数依次为:
,因此前五组的频数依次为: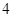 ,
,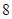 ,
,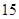 ,
,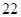 ,
,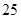 ,根据众数的定义,应是出现次数最多的数,在第五组,用组中值表示该组的值,即为
,根据众数的定义,应是出现次数最多的数,在第五组,用组中值表示该组的值,即为 ,由中位数的定义,应是第
,由中位数的定义,应是第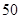 个数与第
个数与第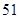 个数的算术平均数,而前四组的频数和:
个数的算术平均数,而前四组的频数和: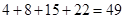 ,是第五组中第1个数与第二个数的算术平均数,对照选项,中位数是
,是第五组中第1个数与第二个数的算术平均数,对照选项,中位数是 最合理,故选B.
最合理,故选B.
考点:1.频率分布直方图;2.中位数与众数的概念.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案学校为了解学生在课外读物方面的支出情况,抽取
了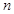 个同学进行调查,结果显示这些同学的支出都在[10,50)(单位:元),其中支出在
个同学进行调查,结果显示这些同学的支出都在[10,50)(单位:元),其中支出在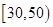 (单位:元)的同学有67人,其频率分布直方图如图所示,则
(单位:元)的同学有67人,其频率分布直方图如图所示,则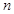 的值为( )
的值为( )
| A.100 | B.120 | C.130 | D.390 |
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设 :“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出
:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出 ,则下列说法正确的( )
,则下列说法正确的( )
| A.这种疫苗能起到预防甲型H1N1流感的有效率为1% |
| B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1 |
| C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
| D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
采用系统抽样方法从960人中抽取32人做问卷调查.为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间 的人做问卷
的人做问卷 ,编号落入区间
,编号落入区间 的人做问卷
的人做问卷 ,其余的人做问卷
,其余的人做问卷 ,则抽到的人中,做问卷
,则抽到的人中,做问卷 的人数为( )
的人数为( )
| A.7 | B.9 | C.10 | D.15 |
下表是甲、乙两个班级进行数学考试,按学生考试及格及不及格统计成绩后的2×2列联表:则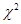 的值为( )
的值为( )
| | 不及格 | 及格 | 合计 |
| 甲班 | 12 | 33 | 45 |
| 乙班 | 9 | 36 | 45 |
| 合计 | 21 | 69 | 90 |
A.0.559 B.0.456 C.0.443 D.0.4
设某大学的女生体重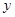 (单位:
(单位: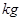 )与身高
)与身高 (单位:
(单位: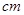 )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据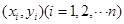 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为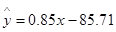 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.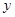 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心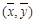 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
| A.6 | B.8 | C.10 | D.12 |
[2013·安徽高考]某班级有50名学生,其中有30名男生和20名女生.随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )
| A.这种抽样方法是一种分层抽样 |
| B.这种抽样方法是一种系统抽样 |
| C.这五名男生成绩的方差大于这五名女生成绩的方差 |
| D.该班男生成绩的平均数小于该班女生成绩的平均数 |
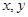 的线性回归方程为( )
的线性回归方程为( )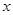
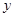
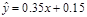 B.
B.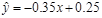
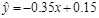 D.
D.