题目内容
已知等比数列
的前n项和为
，若
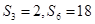，则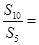
___________.
33
解析试题分析：利用等比数列前
项公式 展开时，需讨论公比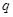
是否为1，∵
，∴
,
,
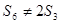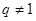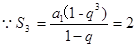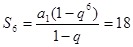,联立得
=
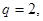
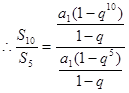
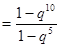=33
考点：等比数列前项和.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
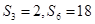已知等比数列的前n项和为，若，则___________.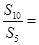
33
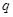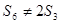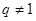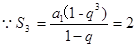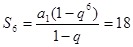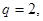
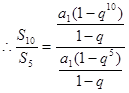
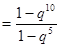解析试题分析：利用等比数列前项公式 展开时，需讨论公比是否为1，∵，∴,,,联立得==33
考点：等比数列前项和.
天天向上一本好卷系列答案小学生10分钟应用题系列答案
满足
=1且
，则
=___________．
；(2)
，则
.
中，
，
，则公比q为 . 
｝的前n项和为
，且
，则使不等式
成立的n的最大值为 ．
的各项均为正数，其前
项和为
．若
，
，
，则
______．
中，
，则公比
等于 
的前
项和为
，它的各项都是正数，且
成等差数列，则
= . 
的各项都为正数，它的前三项依次为1，
，
，则数列
="_____________"