题目内容
如果方程 的两个实根一个小于?1,另一个大于1,那么实数m的取值范围是( )
的两个实根一个小于?1,另一个大于1,那么实数m的取值范围是( )
A. | B.(-2,0) | C.(0,1) | D.(-2,1) |
C
解析试题分析:构建函数f(x)=x2 +(m-1)x+m2-2,根据两个实根一个小于-1,另一个大于1,可得f(-1)<0,f(1)>0,从而可求实数m的取值范围.解:由题意,构建函数f(x)=x2 +(m-1)x+m2-2,∵两个实根一个小于-1,另一个大于1,∴f(-1)<0,f(1)>0,∴0<m<1,故选C
考点:方程根的问题
点评:本题以方程为载体,考查方程根的讨论,关键是构建函数,用函数思想求解.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
若函数f(x) (x∈R)是奇函数,函数g(x) (x∈R)是偶函数,则
| A.函数f[g(x)]是奇函数 | B.函数g[f(x)]是奇函数 |
| C.函数f(x) g(x)是奇函数 | D.函数f(x)+g(x)是奇函数 |
下列函数中,在区间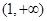 上为增函数的是 ( )
上为增函数的是 ( )
A.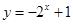 | B.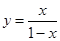 |
C. | D.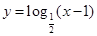 |
下列函数中,在其定义域内既是奇函数又是减函数的是
A. | B. | C. | D. |
下列函数中,在区间 上为增函数的是( ).
上为增函数的是( ).
A.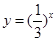 | B.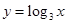 | C.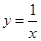 | D.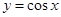 |
下列函数中,在其定义域内既是奇函数又是增函数的是
A.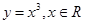 | B.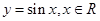 | C.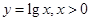 | D.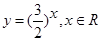 |
 为定义域和值域的函数的图像是( )
为定义域和值域的函数的图像是( )
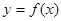 的图象如右下图所示, 则函数
的图象如右下图所示, 则函数 的图象大致为( )
的图象大致为( )

 -2sin x的图象大致是( )
-2sin x的图象大致是( )