题目内容
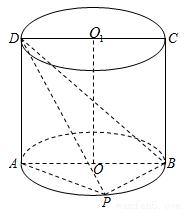
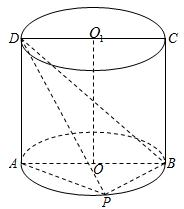如图，ABCD是底面半径为1的圆柱OO1的轴截面，P是下底面圆周上一点（异于A、B）（1）判断A、B、D、P是否在同一个球面上，说明理由；
（2）若DP与底面所成的角是45°，圆柱的体积为
| 3 |
分析：（1）判断A、B、D、P是否在同一个球面上，关键是找出球心，易知线段BD的中点为球心；
（2）首先可知∠BAP是二面角B-AD-P的平面角，利用圆柱的体积，可求二面角B-AD-P的大小．
（2）首先可知∠BAP是二面角B-AD-P的平面角，利用圆柱的体积，可求二面角B-AD-P的大小．
解答：解：（1）在同一球面上，理由：
取线段BD的中点Q，易证△BAD和△BPD都是直角三角形，∴QA=QB=QP=QD，所以A、B、D、P在同一球面上；
（2）依题意，显然∠BAP是二面角B-AD-P的平面角，又DP与底面所成的角是45°，AP=AD=2cos∠BAP，
∴V圆柱=π×1×2cos∠BAP=
π，∴cos∠BAP=
，∴∠BAP=
．
取线段BD的中点Q，易证△BAD和△BPD都是直角三角形，∴QA=QB=QP=QD，所以A、B、D、P在同一球面上；
（2）依题意，显然∠BAP是二面角B-AD-P的平面角，又DP与底面所成的角是45°，AP=AD=2cos∠BAP，
∴V圆柱=π×1×2cos∠BAP=
| 3 |
| ||
| 2 |
| π |
| 6 |
点评：本题以圆柱为载体，考查四点共球，考查面面角，关键是找球心，正确利用公式．
练习册系列答案
相关题目
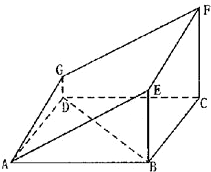如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．
，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°。AB=2AD=2．∠BAD=60。．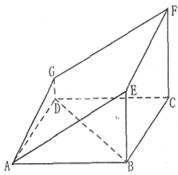
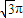，求二面角B-AD-P的大小．