题目内容
(本题满分12分)
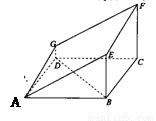
如图的多面体是底面为平行四边形的直四棱柱ABCD— ,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.
,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.
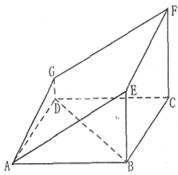
(I)求证:BD⊥平面ADG;
(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值.
【答案】
(Ⅰ)证明:在△BAD中,AB=2AD=2,∠BAD=60°,
由余弦定理得,BD=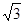
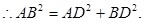
AD⊥BD ----------------------------(2分)
又GD⊥平面ABCD
∴GD⊥BD,
GD AD=D,
AD=D,
∴BD⊥平面ADG……………………4分
(Ⅱ)解:以D为坐标原点,OA为x轴,OB为y轴,OG为z轴建立空间直角坐标系D—xyz
则有A(1,0,0),B(0,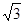 ,0),G(0,0,1),E(0,
,0),G(0,0,1),E(0,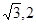 )
)
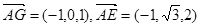 -------------------------------(6分)
-------------------------------(6分)
设平面AEFG法向量为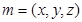
则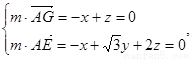
取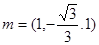 --------------------------------(9分)
--------------------------------(9分)
平面ABCD的一个法向量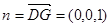 -------------------------(10分)
-------------------------(10分)
设面ABFG与面ABCD所成锐二面角为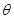 ,
,
则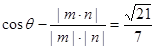 ---------------------------------------(12
---------------------------------------(12
【解析】略

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面