题目内容
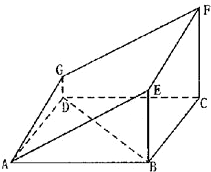 如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.(1)求证:BD⊥平面ADG.
(2)求平面AEFG与平面ABCD所成锐二面角的余弦值.
分析:(1)欲证BD⊥平面ADG,根据直线与平面垂直的判定定理可知只需证BD⊥平面ADG内两相交直线垂直,而AD⊥BD,GD⊥BD,
GD∩AD=D,满足定理条件;
(2)以D为坐标原点,OA为x轴,OB为y轴,OG为z轴建立空间直角坐标系D-xyz,分别求出平面AEFG法向量和平面ABCD的一个法向量,然后求出两法向量的夹角的余弦值,即可求出平面AEFG与平面ABCD所成锐二面角的余弦值.
GD∩AD=D,满足定理条件;
(2)以D为坐标原点,OA为x轴,OB为y轴,OG为z轴建立空间直角坐标系D-xyz,分别求出平面AEFG法向量和平面ABCD的一个法向量,然后求出两法向量的夹角的余弦值,即可求出平面AEFG与平面ABCD所成锐二面角的余弦值.
解答:解:(1)证明:在△BAD中,AB=2AD=2,∠BAD=60°,
由余弦定理得,BD=
∴AB2=AD2+BD2.
∴AD⊥BD(2分)
又GD⊥平面ABCD
∴GD⊥BD,
GD∩AD=D,
∴BD⊥平面ADG(4分)
(2)以D为坐标原点,OA为x轴,OB为y轴,OG为z轴建立空间直角坐标系D-xyz
则有A(1,0,0),B(0,
,0),G(0,0,1),E(0,
,2)
=(-1,0,1),
=(-1,
,2)(6分)
设平面AEFG法向量为m=(x,y,z)
则
,
取m=(1,-
.1)(9分)
平面ABCD的一个法向量n=
=(0,0,1)(10分)
设面ABFG与面ABCD所成锐二面角为θ,
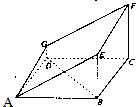
则cosθ-
=
(12分)
∴平面AEFG与平面ABCD所成锐二面角的余弦值为
.
由余弦定理得,BD=
| 3 |
∴AD⊥BD(2分)
又GD⊥平面ABCD
∴GD⊥BD,
GD∩AD=D,
∴BD⊥平面ADG(4分)
(2)以D为坐标原点,OA为x轴,OB为y轴,OG为z轴建立空间直角坐标系D-xyz
则有A(1,0,0),B(0,
| 3 |
| 3 |
| AG |
| AE |
| 3 |
设平面AEFG法向量为m=(x,y,z)
则
|
取m=(1,-
| ||
| 3 |
平面ABCD的一个法向量n=
| DG |
设面ABFG与面ABCD所成锐二面角为θ,

则cosθ-
| |m•n| |
| |m|•|n| |
| ||
| 7 |
∴平面AEFG与平面ABCD所成锐二面角的余弦值为
| ||
| 7 |
点评:本题主要考查了直线与平面垂直的判定,以及二面角及其度量,二面角在最近高考中有所弱化,值得大家主要.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目


 ,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.
,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.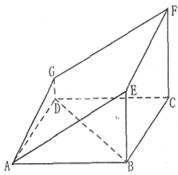
 ,经平面AEFG
,经平面AEFG


