题目内容
(2012•奉贤区二模)过平面区域
内一点P作圆O:x2+y2=1的两条切线,切点分别为A,B,记∠APB=α,当α最小时,此时点P坐标为
|
(-4,-2)
(-4,-2)
.分析:先依据不等式组
,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用圆的方程画出图形,确定α最小时点P的位置即可.
|
解答: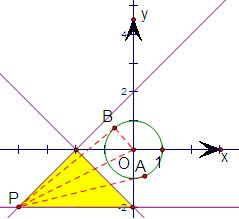 解:如图阴影部分表示
解:如图阴影部分表示
,确定的平面区域,
当P离圆O最远时,α最小,
此时点P坐标为:(-4,-2),
故答案为::(-4,-2).
 解:如图阴影部分表示
解:如图阴影部分表示
|
当P离圆O最远时,α最小,
此时点P坐标为:(-4,-2),
故答案为::(-4,-2).
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•奉贤区二模)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为
(2012•奉贤区二模)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为