题目内容
已知函数
 ,
,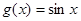 .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)当 时
时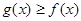 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)若 ,求证:
,求证: .
.

 ,
,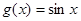 .
.(1)若
 ,求函数
,求函数 的极值;
的极值;(2)当
 时
时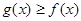 恒成立,求
恒成立,求 的取值范围;
的取值范围;(3)若
 ,求证:
,求证: .
.(1) -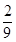 (2)
(2) 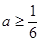 (3)见解析
(3)见解析
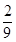 (2)
(2) 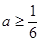 (3)见解析
(3)见解析本试题主要是考查了导数在研究函数中的运用。
(1) 函数
 ,
,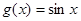 .因为
.因为 ,求解函数
,求解函数 的导数得到极值;
的导数得到极值;
(2)当 时
时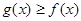 恒成立,只要构造新函数
恒成立,只要构造新函数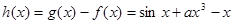 ,利用导数判定单调性得到证明。
,利用导数判定单调性得到证明。
(3) 由(2)知当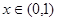 时有
时有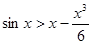 即
即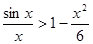
所以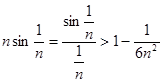
然后利用放缩法的思想得到证明。.
解:(1)极大值为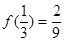 ,极小值为
,极小值为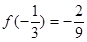 …………………….4分
…………………….4分
(2)设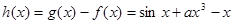
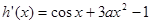
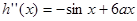
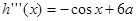
注意到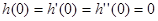
若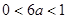 即
即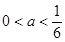 ,
, ,使
,使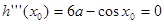
这与题目要求矛盾.
若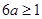 即
即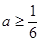 , 当
, 当 时
时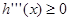 ,进而
,进而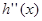 在
在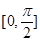 上递增,从而
上递增,从而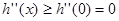 ,于是
,于是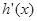
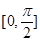 上递增,所以
上递增,所以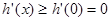 ,故
,故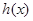 在
在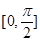 上递增,所以
上递增,所以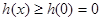 恒成立,满足题目要求.
恒成立,满足题目要求.
综上所述, 的取值范围是
的取值范围是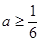 ………………………………………………..9分
………………………………………………..9分
(3)由(2)知当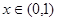 时有
时有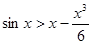 即
即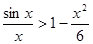
所以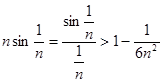
从而
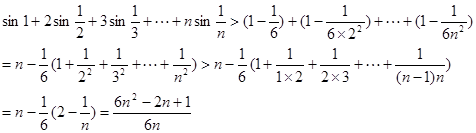
证毕……………………14分
(1) 函数

 ,
,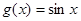 .因为
.因为 ,求解函数
,求解函数 的导数得到极值;
的导数得到极值;(2)当
 时
时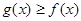 恒成立,只要构造新函数
恒成立,只要构造新函数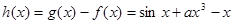 ,利用导数判定单调性得到证明。
,利用导数判定单调性得到证明。(3) 由(2)知当
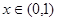 时有
时有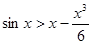 即
即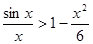
所以
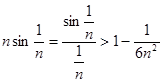
然后利用放缩法的思想得到证明。.
解:(1)极大值为
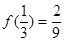 ,极小值为
,极小值为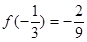 …………………….4分
…………………….4分(2)设
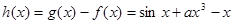
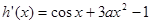
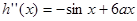
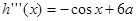
注意到
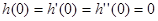
若
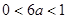 即
即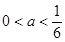 ,
, ,使
,使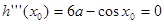
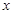 | 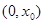 | 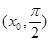 |
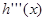 | 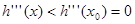 | 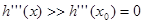 |
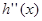 | 递减,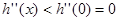 | |
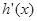 | 递减,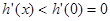 | |
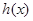 | 递减,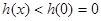 | |
若
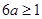 即
即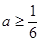 , 当
, 当 时
时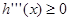 ,进而
,进而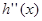 在
在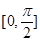 上递增,从而
上递增,从而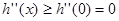 ,于是
,于是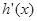
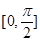 上递增,所以
上递增,所以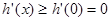 ,故
,故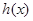 在
在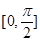 上递增,所以
上递增,所以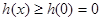 恒成立,满足题目要求.
恒成立,满足题目要求.综上所述,
 的取值范围是
的取值范围是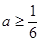 ………………………………………………..9分
………………………………………………..9分(3)由(2)知当
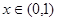 时有
时有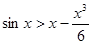 即
即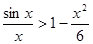
所以
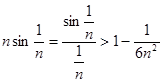
从而
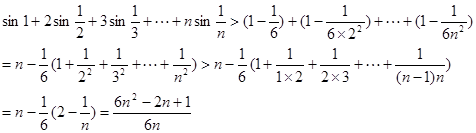
证毕……………………14分

练习册系列答案
相关题目
 (
( ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
. 的值;
的值;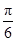 个单位后,得到函数
个单位后,得到函数 的图象,求
的图象,求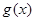 的单调递减区间.
的单调递减区间.  为最小正周期的偶函数是( )
为最小正周期的偶函数是( )



 作怎样的变换可得到函数
作怎样的变换可得到函数 ( )
( ) 个单位
个单位  个单位
个单位  )图象可以看作把函数y=3sin2x的图象作下列移动而得到( )
)图象可以看作把函数y=3sin2x的图象作下列移动而得到( ) 单位
单位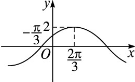
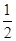 ,φ=-
,φ=-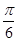
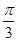
 中,
中, ,则角
,则角 为( )
为( ) 
 的最小正周期为
的最小正周期为 




 的图象的一条对称轴是( )
的图象的一条对称轴是( )


