题目内容
已知抛物线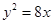 上一点P到y轴的距离为5,则点P到焦点的距离为( )
上一点P到y轴的距离为5,则点P到焦点的距离为( )
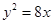 上一点P到y轴的距离为5,则点P到焦点的距离为( )
上一点P到y轴的距离为5,则点P到焦点的距离为( )| A.5 | B.6 | C.7 | D.8 |
C
试题分析:因为抛物线
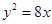 的焦点坐标为(2,0),因为P(5,y)到焦点距离等于到准线的距离,又因为抛物线的准线方程为
的焦点坐标为(2,0),因为P(5,y)到焦点距离等于到准线的距离,又因为抛物线的准线方程为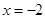 .所以P点到准线的距离为5+2="7." 即点P到焦点的距离为7.故选C.本小题关键是抛物线的定义的应用.
.所以P点到准线的距离为5+2="7." 即点P到焦点的距离为7.故选C.本小题关键是抛物线的定义的应用.
练习册系列答案
相关题目
题目内容
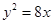 上一点P到y轴的距离为5,则点P到焦点的距离为( )
上一点P到y轴的距离为5,则点P到焦点的距离为( )| A.5 | B.6 | C.7 | D.8 |
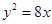 的焦点坐标为(2,0),因为P(5,y)到焦点距离等于到准线的距离,又因为抛物线的准线方程为
的焦点坐标为(2,0),因为P(5,y)到焦点距离等于到准线的距离,又因为抛物线的准线方程为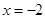 .所以P点到准线的距离为5+2="7." 即点P到焦点的距离为7.故选C.本小题关键是抛物线的定义的应用.
.所以P点到准线的距离为5+2="7." 即点P到焦点的距离为7.故选C.本小题关键是抛物线的定义的应用.