题目内容
 如图所示,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线x=t(0≤t≤2)截这个三角形可得位于此直线左方的图形(阴影部分)的面积为f(t),则函数 y=f(t)的图象(如下图所示)大致是( )
如图所示,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线x=t(0≤t≤2)截这个三角形可得位于此直线左方的图形(阴影部分)的面积为f(t),则函数 y=f(t)的图象(如下图所示)大致是( )分析:求出点A的坐标,分0≤t≤1和1≤t≤2两种情况,分别求出这个三角形可得位于此直线左方的图形的面积f(t)的解析式,根据函数解析式判断其曲线形状.
解答:解:点A的坐标为(1,
),当 0≤t≤1时,这个三角形可得位于此直线左方的图形的面积f(t)=
•t•2t•
=
t2,
当1≤t≤2时,面积f(t)=
×2×
-
(2-t)•
(2-t)=-
t2+2
t-
=-
(t-2)2
它的图象如图④所示:
故答案为 ④.
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
当1≤t≤2时,面积f(t)=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| ||
| 2 |
它的图象如图④所示:
故答案为 ④.
点评:本题主要考查求函数的解析式以及根据函数的解析式判断函数的图象形状,体现了分类讨论、数形结合的数学思想.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
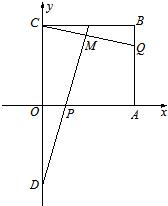 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2, (2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
(2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB. ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.
 ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.
 ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.