题目内容
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2, ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.(Ⅰ)求点M的轨迹方程;
(Ⅱ)若过点(1,0)的直线与点M的轨迹相交于E,F两点,求△AEF的面积的最大值.

【答案】分析:(1)由向量运算得到直线DP的方程和直线CQ的方程,消去参数即可得到M的轨迹方程;
(2)欲求△AEF的面积的最大值,先将△AEF的面积表示成某个变量的函数,再利用基本不等式求函数的最大值即可.
解答:解:(Ⅰ)设点M的坐标为(x,y),由图可知A(2,0), ,
, ,
, .
.
由 ,得点P的坐标为(2λ,0);
,得点P的坐标为(2λ,0);
由 ,得点Q的坐标为
,得点Q的坐标为 .
.
于是,当λ≠0时,直线DP的方程为 ,①
,①
直线CQ的方程为 .②
.②
①×②,得 ,即
,即 .
.
当λ=0时,点M即为点C,而点C的坐标 也满足上式.
也满足上式.
故点M的轨迹方程为 .
.
(Ⅱ)设过点(1,0)的直线EF的方程为x=my+1,且设E(x1,y1),F(x2,y2).
由
得(3m2+4)y2+6my-9=0.③
由于上述方程的判别式△=(6m)2+36(3m2+4)>0,所以y1,y2是方程③的两根,
根据求根公式,可得 .
.
又A(2,0),所以△AEF的面积 .
.
令 (t≥1),则m2=t2-1.
(t≥1),则m2=t2-1.
于是 ,t≥1.
,t≥1.
记 ,t≥1,则
,t≥1,则 .
.
因为当t≥1时,f'(t)>0,所以 在[1,+∞)上单调递增.
在[1,+∞)上单调递增.
故当t=1时,f(t)取得最小值 ,
,
此时 取得最大值
取得最大值 .
.
综上所述,当m=0时,即直线EF垂直于x轴时,△AEF的面积取得最大值 .
.
点评:本小题主要考查向量的运算、直线方程、求曲线的方程以及函数最值等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.
(2)欲求△AEF的面积的最大值,先将△AEF的面积表示成某个变量的函数,再利用基本不等式求函数的最大值即可.
解答:解:(Ⅰ)设点M的坐标为(x,y),由图可知A(2,0),
 ,
, ,
, .
.由
 ,得点P的坐标为(2λ,0);
,得点P的坐标为(2λ,0);由
 ,得点Q的坐标为
,得点Q的坐标为 .
.于是,当λ≠0时,直线DP的方程为
 ,①
,①直线CQ的方程为
 .②
.②①×②,得
 ,即
,即 .
.当λ=0时,点M即为点C,而点C的坐标
 也满足上式.
也满足上式.故点M的轨迹方程为
 .
.(Ⅱ)设过点(1,0)的直线EF的方程为x=my+1,且设E(x1,y1),F(x2,y2).
由

得(3m2+4)y2+6my-9=0.③
由于上述方程的判别式△=(6m)2+36(3m2+4)>0,所以y1,y2是方程③的两根,
根据求根公式,可得
 .
.又A(2,0),所以△AEF的面积
 .
.令
 (t≥1),则m2=t2-1.
(t≥1),则m2=t2-1.于是
 ,t≥1.
,t≥1.记
 ,t≥1,则
,t≥1,则 .
.因为当t≥1时,f'(t)>0,所以
 在[1,+∞)上单调递增.
在[1,+∞)上单调递增.故当t=1时,f(t)取得最小值
 ,
,此时
 取得最大值
取得最大值 .
.综上所述,当m=0时,即直线EF垂直于x轴时,△AEF的面积取得最大值
 .
.点评:本小题主要考查向量的运算、直线方程、求曲线的方程以及函数最值等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
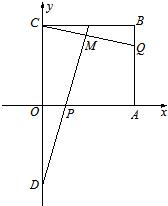 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2, (2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
(2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB. ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.
 ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.