题目内容
如图,点M,N是边长为4的正△ABC的边AB,AC的中点,现将△AMN沿MN折起,使平面AMN⊥平面BCNM.在四棱锥A—BCNM中,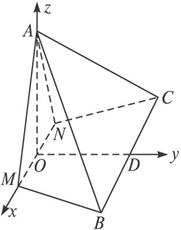
(1)求异面直线AM与BC所成的角;
(2)求直线BA与平面ANC所成角的正弦值;
(3)在线段AB上,是否存在一个点Q,使MQ⊥平面ABC?若存在,试确定点Q的位置;若不存在,请说明理由.
解:(1)∵BC∥MN,∠AMN就是异面直线AM与BC所成的角,
∴异面直线AM与BC所成的角为60°.
(2)取MN,BC的中点为O,D,
这时OD⊥MN,平面AMN⊥平面BCNM,
∴AO⊥平面BCNM.
分别以直线NM,OD,OA为x轴,y轴,z轴,建立空间直角坐标系,如图,

则A(0,0,![]() ),B(2,
),B(2,![]() ,0),C(-2,
,0),C(-2,![]() ,0),N(-1,0,0),M(1,0,0).
,0),N(-1,0,0),M(1,0,0).
设平面ANC的法向量为n=(x,y,z),
则![]()
∴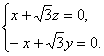
取n=(x,y,z)=(3,![]() ,-
,-![]() ),又
),又![]() =(2,
=(2,![]() ,-
,-![]() ).
).
从而cos〈n,![]() 〉=
〉=![]() ,
,
∴直线BA与平面ANC所成角的正弦值为![]() .
.
(3)假设在线段AB上存在Q(x,y,z),
设![]() =λ
=λ![]() ,
,
则(x-2,y-![]() ,z)=λ(-2,-
,z)=λ(-2,-![]() ,
,![]() ),
),
这时x=2-2λ,y=![]() -
-![]() λ,z=
λ,z=![]() λ,
λ,
从而MQ=(1-2λ,![]() -
-![]() λ,
λ,![]() λ),
λ),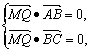 解得λ=
解得λ=![]() .
.
∴存在点Q,使MQ⊥平面ABC,点Q是AB的中点.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
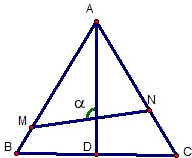 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a(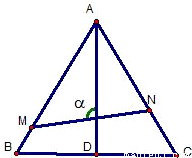 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(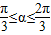 )
)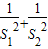 的最大值与最小值.
的最大值与最小值. 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a( )
) 的最大值与最小值.
的最大值与最小值. ).
). 
 的最大值与最小值.
的最大值与最小值.